Anatomía de una prueba t perfecta

En mi reciente vuelta a Twitter, he empezado a seguir al profesor responsable del excelente MOOC “Improving your statistical inferences” (enlace), Daniël Lakens (@lakens), que comparte más que interesantes perlas relacionadas con el campo de la estadística.

Hace unos días anunciaba que había actualizado un script para R cuyo nombre no tiene desperdicio: “Perfect t-test”. Las principales referencias que tenemos que consultar son:

• The perfect t-test.
• Repositorio en GitHub con el código asociado al anterior artículo.

Como no podía ser de otra manera, un recurso así despierta enormemente tanto mi curiosidad, como las ganas de echar un rato explorando las posibilidades que ofrece.

Ahora bien, ¿de qué trata todo el asunto? Estamos ante un documento escrito con R Markdown cuyo objetivo es automatizar el proceso de comparación de medias para dos muestras, tanto independientes como dependientes (cada caso tiene su archivo asociado). No obstante, cuando la mayoría de programas informáticos orientados al análisis de datos ya incorporan este tipo de herramienta, ¿qué justifica la existencia de este recurso?

Según el autor, no todos los investigadores siguen las recomendaciones que los estadísticos indican (o bien no están al día de las mismas), e incluso, hecho que personalmente considero más grave, los propios programas informáticos ignoran dichas recomendaciones en ocasiones.

Dentro del “peligro” que supone emplear algoritmos que automatizan análisis de datos, que pueden provocar que llevemos a cabo todo tipo de acciones sin saber muy bien las razones para ello, dado que los vamos a utilizar igualmente, siempre será más recomendable que escojamos aquellos que mejor diseñados estén, ¿verdad?

Veamos qué nos ofrece el código de Daniël Lakens. Una vez digerido el README del repositorio, e instalado los paquetes necesarios (así como actualizado JAGS, que aún estaba utilizando la versión 3), sólo tengo que encontrar algún conjunto de datos que me permita llevar a cabo una prueba t.

He escogido el conjunto de datos hsb2 (incluido en el paquete openintro), que está formado por los registros de una encuesta realizada a 200 estudiantes de secundaria. Vamos a investigar una simple cuestión, ¿existen diferencias en las puntuaciones, asociadas a matemáticas, entre chicos y chicas? Para resolver el interrogante, lo primero que debemos hacer es generar un archivo de texto que contenga los datos de interés, siguiendo el formato que se nos especifica en el archivo perfect_independent_t-test.Rmd.

# Carga la librería que contiene el conjunto de datos hsb2
library(openintro)

# Carga el conjunto de datos hsb2
data(hsb2)

# Documentación del conjunto de datos
?hsb2

# Exploración básica del conjunto de datos
str(hsb2)

# Crea el archivo que se usará con "perfect_independent_t-test.Rmd"
write.table(hsb2[c("id", "gender", "math")],
            file = "datos_hsb2_math.txt",
            row.names = FALSE,
            sep = ",")

Nota: en lugar de crear un archivo de texto cuyas columnas estuvieran delimitadas por tabuladores, escogí utilizar comas. Eso luego implica realizar modificaciones menores en el fichero de la prueba t.

Ahora, con datos_hsb2_math.txt ubicado en el mismo directorio que perfect_independent_t-test.Rmd, únicamente tenemos que actualizar la ruta que aparece en la línea 62 para la variable alldata (y, en mi caso, añadir sep = ","), así como correctamente asignar las variables xlabel, ylabel, factorlabel, measurelabel, xlabelstring e ylabelstring siguiendo las instrucciones. El resto de variables, para una primera aproximación a esta herramienta, podemos dejarlas con los valores que han recibido por defecto.

En mi caso, he cambiado el formato del documento de salida de Word a PDF, y, tras pulsar el botón correspondiente, he acabado con un documento ¡de 15 páginas para una simple prueba t! A la próxima persona que escuche quejarse de que SPSS devuelve una miríada de resultados voy a invitarle amablemente a que utilice este script.

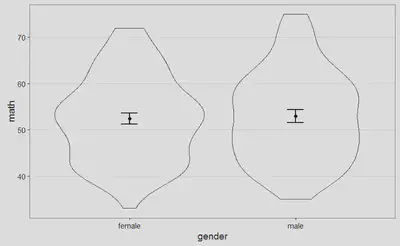
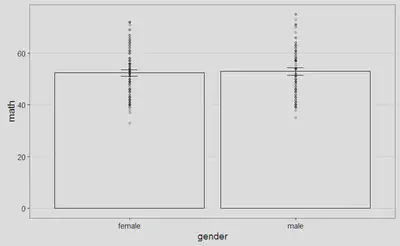
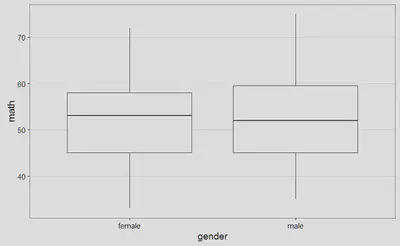
Sin embargo, una vez superado el susto inicial, gran parte del documento son explicaciones generales que justifican el modo de proceder seguido. La primera figura que encontramos es el siguiente boxplot (creo que en español se llama diagrama de caja y bigotes, pero no estoy completamente seguro), con el objeto de identificar la existencia de posibles valores atípicos:

A continuación, se realizan cuatro contrastes de hipótesis para comprobar si se verifica el supuesto de normalidad para las puntuaciones de ambos grupos (su violación tiene efectos, por ejemplo, sobre el error de tipo I):

En uno de los cuatros contrastes, los datos con los que estamos trabajando aportan evidencia suficiente para sospechar de la veracidad de la hipótesis nula (“las puntuaciones siguen una distribución normal”), por lo que tendríamos que preferiblemente recurrir a métodos no paramétricos o estadísticos robustos. No obstante, en el propio documento nos avisan de que con muestras grandes (y podemos considerar que la dada lo es) este tipo de situaciones pueden presentarse.

Podemos examinar la distribución de puntuaciones, para cada uno de los grupos, de manera gráfica, a partir de las siguientes figuras, y juzgar así cómo se desvían nuestros datos (línea negra) de la distribución normal asociada (línea discontinua roja):

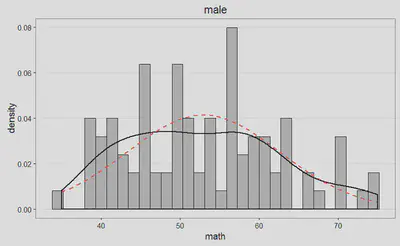
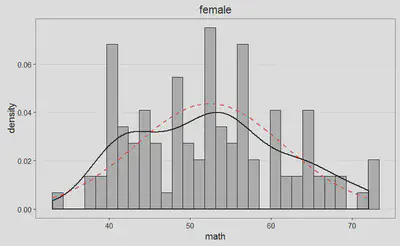
Por si las anteriores figuras todavía no resolvieran el interrogante, tenemos a nuestra disposición los siguientes gráficos Q-Q:

No resulta por tanto descabellado aceptar que se verifica el supuesto de normalidad para los datos dados. Pasemos ahora a estudiar la hipótesis de igualdad de varianzas entre los grupos considerados. Para ello, utilizaremos la prueba de Levene, que en nuestro caso particular concluye:

Levene’s test for equality of variances (p = 0.46) indicates that the assumption that variances are equal is not rejected.

A continuación encontramos la sección de resultados donde, siguiendo el estilo de publicación de las revistas científicas, se recogen las conclusiones para la prueba t que hemos llevado a cabo. Aquí, en función de la filosofía con la que solamos trabajar y de si se verifican las condiciones asociadas a esta prueba, tendremos que escoger entre la sección dedicada a estadísticos frecuentistas, bayesianos o robustos. Por ejemplo, para la primera opción encontraríamos:

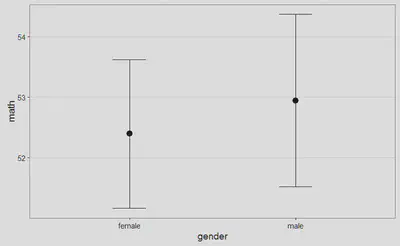
The mean math of participants in the male condition (M = 52.95, SD = 9.66, n = 91) was greater than the mean of participants in the female condition (M = 52.39, SD = 9.15, n = 109). The difference between the two measurements (M = 0.55, 95% CI = [-2.09;3.19]) was analyzed with Welch’s t-test, t(187.58) = 0.41, p = 0.682, Hedges’ g = 0.06, 95% CI [-0.22;0.34]. This can be considered a tiny effect. The observed data is not surprising under the assumption that the null-hypothesis is true. The Common Language effect size (McGraw & Wong, 1992) indicates that the likelihood that the math of a random person in the male condition is greater than the math of a random person in the female condition is 52%.

Tenemos a nuestra disposición la media, la desviación estándar y el tamaño muestral para cada uno de los grupos considerados. A continuación encontramos el valor del estadístico asociado a la prueba t de Welch, así como su correspondiente p-valor. Como indicador del tamaño del efecto encontramos la g de Hedges. Sin embargo, al margen del aluvión de valores con el que ya seríamos capaces de dar respuesta al interrogante que ha motivado este artículo (¿seríamos de verdad capaces?), me ha encantado la parte final de este párrafo, donde nos transmiten con palabras llanas qué conclusiones deberíamos extraer.

El documento añade los gráficos que mostraré a continuación, así como las referencias para las justificaciones vertidas a lo largo de él, el propio conjunto de datos y cierta información técnica de la sesión de trabajo en R. Es un estupendo recurso para tener siempre disponible a mano, ¿verdad?