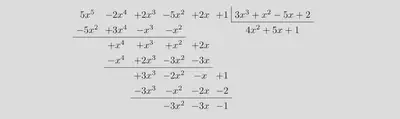¿Cómo dividir polinomios con LaTeX en conjuntos finitos?

La semana anterior analizamos el paquete polynom, que nos permite fácilmente llevar a cabo la transcripción de divisiones de polinomios con LaTeX. A continuación, estudiaremos una manera alternativa para lidiar con este asunto que, además, nos permitirá operar en conjuntos finitos.

Supongamos, sin pérdida de generalidad, que nuestro objetivo es dividir los polinomios

$$ 5x^5 - 2x^4 + 2x^3 - 5x^2 + 2x + 1 $$

y

$$ 3x^3 + x^2 - 5x + 2 $$

en $\mathbb{Z}_7$. Para ello, ‘‘dibujaremos’’ la operación matemática en una matriz, método que nos permitirá organizar fácilmente los pasos y, de paso, imprimir algunas rayas horizontales cuando proceda.

Para empezar, en el preámbulo del documento, insertamos las dos siguientes líneas:

\usepackage{tikz}
\usetikzlibrary{matrix}

Ahora, donde deseemos ubicar la división de los anteriores polinomios, tecleamos:

\begin{center}
\begin{tikzpicture}
\matrix (a) [matrix of math nodes, column sep=0pt]
{
5x^5 & -2x^4 & +2x^3 & -5x^2 & +2x & +1 &  & 3x^3+x^2-5x+2 \\
};
\draw (a-1-8.north west) |- (a-1-8.south east);
\end{tikzpicture}
\end{center}

dando el resultado que figura en la siguiente imagen:

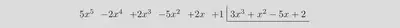
Organizar los monomios del dividendo como elementos individuales de una matriz nos facilitará la empresa de ‘‘alinear’’ las posteriores operaciones de la división. Por otro lado, el comando draw es el que dibuja la ‘‘caja’’ de esta operación matemática, tomando como referencia las posiciones de los elementos de la matriz.

Continuemos la división, siempre teniendo en cuenta que trabajamos en $\mathbb{Z}_7$. Así, para la primera etapa, teclearíamos acto seguido:

\begin{center}
\begin{tikzpicture}
\matrix (a) [matrix of math nodes, column sep=0pt]
{
 5x^5 & -2x^4 & +2x^3 & -5x^2 & +2x & +1 &  & 3x^3+x^2-5x+2 \\
-5x^2 & +3x^4 &  -x^3 &  -x^2 &     &    &  & 4x^2\\
      &  +x^4 &  +x^3 &  +x^2 & +2x &    &  & \\
};
\draw (a-1-8.north west) |- (a-1-8.south east);
\draw (a-2-1.south west) -- (a-2-4.south east);
\end{tikzpicture}
\end{center}

cuyo resultado se recoge en la siguiente figura:

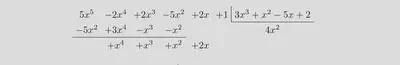
Efectivamente, no queda tan estético como el que conseguíamos la semana pasada con el paquete polynom. No obstante, funcionalmente hablando, los pequeños desajustes horizontales de signos no molestan en exceso.

Una vez asimilada la idea del procedimiento a seguir, únicamente nos resta continuar con la división, escribiendo ahora:

\begin{center}
\begin{tikzpicture}
\matrix (a) [matrix of math nodes, column sep=0pt]
{
 5x^5 & -2x^4 & +2x^3 & -5x^2 & +2x & +1 &  & 3x^3+x^2-5x+2 \\
-5x^2 & +3x^4 &  -x^3 &  -x^2 &     &    &  & 4x^2 + 5x + 1\\
      &  +x^4 &  +x^3 &  +x^2 & +2x &    &  & \\
      &  -x^4 & +2x^3 & -3x^2 & -3x &    &  & \\
      &       & +3x^3 & -2x^2 &  -x & +1 &  & \\
      &       & -3x^3 &  -x^2 & -2x & -2 &  & \\
      &       &       & -3x^2 & -3x & -1 &  & \\
};
\draw (a-1-8.north west) |- (a-1-8.south east);
\draw (a-2-1.south west) -- (a-2-4.south east);
\draw (a-4-2.south west) -- (a-4-5.south east);
\draw (a-6-3.south west) -- (a-6-6.south east);
\end{tikzpicture}
\end{center}

Obteniendo como resultado el que aparece en la siguiente imagen: