Combinatoria

Problemas resueltos

Problema 1

• (a) ¿De cuántas formas se pueden sentar ocho personas en una fila de ocho asientos?
• (b) ¿Cuántas palabras distintas de diez letras se pueden formar con las letras $A$, $B$, $C$ y $D$?
• (c) ¿De cuántas formas pueden huir diez niños de la policía en un cruce de calles?
• (d) ¿Cuántas distribuciones se pueden conseguir lanzando diez monedas?
• (e) ¿De cuántas formas se pueden obtener cinco caras y cinco cruces en el apartado anterior?
• (f) ¿Cuántos números de $4$ cifras se pueden formar con los dígitos $1,2,3,\ldots, 9$?
• (g) ¿Cuántas distribuciones de cumpleaños pueden darse entre diez amigos?

Solución: para el apartado (a), dado que el orden importa y utilizamos todos los elementos, sin que ninguno de ellos se repita, buscamos la cantidad de permutaciones de ocho elementos. Así, $P_8 = 8! = 40320$ es el número de formas en que se pueden sentar ocho personas en una fila de ocho asientos.

En el apartado (b), el orden vuelve a importar y, obviamente, hemos de permitir la repetición de las letras para conformar las palabras, por lo que ahora la herramienta adecuada para contar será el total de variaciones de cuatro elementos tomadas de diez en diez. Por tanto, hay

$$ VR_{4,10} = 4^{10} = 1048576 $$

palabras distintas de diez letras conformadas a partir de las letras $A$, $B$, $C$ y $D$.

En cuanto al apartado (c), hemos de ser cautos a la hora de escoger quién juega el papel de los ‘’elementos’’ para contabilizar el total de maneras en que realizar la acción. En esta ocasión, son las calles. Si consideramos un cruce estándar de cuatro de ellas (y las denotamos por $a$, $b$, $c$ y $d$), una posible forma de escapar de la policía consistiría en que todos los niños optasen por la calle $a$, generando así el valor $(a,a,\ldots,a)$. Si el primer niño escogiese la calle $b$ y el resto la $a$, tendríamos el valor $(b,a,a,\ldots,a)$, y así sucesivamente. Por tanto, como importa el orden y alguna de las calles estará repetida dentro de las opciones de la huida, buscamos el número de variaciones con repetición de cuatro elementos tomados de diez en diez. Como antes, $VR_{4,10} = 4^{10}$ es el número de formas en que pueden huir diez niños de la policía en un cruce de calles.

Para el apartado (d), un tanto ambiguo, asumiremos que están interesados en conocer el número de secuencias de caras y cruces que se pueden encontrar lanzando diez monedas. Con esta reformulación, es claro que son dos los elementos protagonistas, cara y cruz, y consideraremos que el orden importa porque, suponemos, las monedas son distinguibles. Por tanto, buscamos el número de variaciones con repetición de dos elementos tomados de diez en diez, esto es, hay $VR_{2,10} = 2^{10} = 1024$ posibles secuencias de caras y cruces cuando se lanzan diez monedas.

A continuación, en el apartado (e), como el orden continúa siendo importante y cada elemento se repite un número fijo de veces, estamos interesados en la cantidad de permutaciones con repetición de diez elementos, donde tanto un elemento, como el otro, se repite en cinco ocasiones. Es decir, hay

$$ P(10;5,5) = PR_{10}^{5,5} = \dfrac{10!}{5!\cdot 5!} = \dfrac{10\cdot9\cdot8\cdot7\cdot6}{5!} = 252 $$

formas de obtener cinco caras y cinco cruces al lanzar diez monedas.

En el apartado (f) hemos de considerar dos opciones posibles, en función de si admitimos o no repetición de los números. En caso afirmativo, al importar el orden y permitir repetición de los números, estamos interesados en el número de variaciones con repetición de nueve elementos tomados de cuatro en cuatro, esto es, hay $VR_{9,4} = 9^4 = 6561$ números de cuatro cifras conformados a partir de los dígitos $1,2,3,\ldots,9$ que pueden poseer, además, dígitos repetidos. En caso negativo, el orden continúa siendo importante, pero ahora no permitimos la repetición de cifras, por lo que estamos interesados en hallar el número de variaciones de nueve elementos tomados de cuatro en cuatro, es decir, $V_{9,4} = 9\cdot8\cdot7\cdot6 = 3024$ posibilidades.

Finalmente, en el apartado (g), si todos los amigos celebrasen su cumpleaños el primer día del año, se generaría el valor $(1,1,\ldots,1)$. Si el primer amigo lo celebrase el quinto día del año y el resto el tercer día, se conformaría el valor $(5,3,3\ldots,3)$. Así, vemos que los elementos son los días del año, $365$, que los vamos a tomar de diez en diez. Como admitimos la posibilidad de que dos amigos cumplan año el mismo día, esto es, de repetir elemento, e importa el orden, estamos interesados en hallar el número de variaciones con repetición de $365$ elementos tomados de diez en diez. Así, hay $VR_{365,10} = 365^{10}$ distribuciones de cumpleaños posibles entre los diez amigos.

Problema 2

Considerando una baraja de póquer de $52$ cartas,

• (a) ¿cuántas manos de cinco cartas se pueden extraer?
• (b) De las manos anteriores, ¿cuántas tienen tres ases?
• (c) De estas últimas, ¿cuántas serán full?
• (d) En general, ¿cuántos full podemos extraer de la baraja?
• (e) ¿Y cuántas manos contienen una doble pareja?

Solución: de cara al apartado (a), como no importa el orden en el que recibamos las cartas en una mano cualquiera y no existe la posibilidad de recibir cartas recibidas, estamos interesados en calcular el número de combinaciones de $52$ elementos tomados de cinco en cinco. Así, hay

$$ \dbinom{52}{5} = \dfrac{52!}{5!\cdot47!} = \dfrac{52\cdot51\cdot50\cdot49\cdot48}{5!} = 2598960 $$

manos posibles de cinco cartas que podemos extraer de una baraja de póquer de $52$ cartas.

En cuanto al apartado (b), razonaremos como sigue: de los cuatro ases que posee la baraja, tomamos tres de ellos. Como no importa el orden en el que los extraigamos y no habrá ninguno repetido, esta acción la podemos llevar a cabo de

$$ \dbinom{4}{3} = \dfrac{4!}{3!\cdot1!} = 4 $$

formas posibles. Ahora, del resto de cartas de la baraja que no son ases, $52-4=48$, simplemente hemos de tomar dos cartas adicionales, situación que puede darse de

$$ \dbinom{48}{2} = \dfrac{48!}{2!\cdot46!} = \dfrac{48\cdot47}{2} = 1128 $$

maneras posibles. Aplicando la regla del producto, hay

$$ \dbinom{4}{3}\cdot\dbinom{48}{2} = 4\cdot1128 = 4512 $$

manos que poseen tres ases.

Siguiendo con el apartado (c), para conformar un full a partir de tres ases necesitamos que las otras dos cartas (distintas ambas del as) posean idéntico número. Así, empecemos tomando nuestros tres ases, que sabemos es una acción que podemos llevar a cabo de

$$ \dbinom{4}{3} = \dfrac{4!}{3!\cdot1!} = 4 $$

formas posibles. Ahora, de los doce números distintos de cartas que restan, seleccionamos uno en particular ($C_{12,1}$) y, de las cuatro cartas posibles asociadas a dicho número, tomamos dos ($C_{4,2}$). Aplicando la regla del producto, existen

$$ \dbinom{12}{1}\cdot\dbinom{4}{2} = 12\cdot\dfrac{4!}{2!\cdot2!} = 72 $$

maneras de realizar la anterior elección. Finalmente, utilizando de nuevo la regla del producto, hay

$$ \dbinom{4}{3}\cdot\dbinom{12}{1}\cdot\dbinom{4}{2} = 4\cdot72 = 288 $$

manos con $3$ ases que son full.

Para el apartado (d), la manera de razonar es muy similar a la mostrada en el párrafo anterior. De los $13$ números posibles, seleccionamos uno de ellos ($C_{13,1}$) y será de este del que tomaremos tres cartas iguales ($C_{4,3}$). Ahora de los $12$ números restantes, escogemos uno ($C_{12,1}$) y extraemos luego dos cartas idénticas ($C_{4,2}$). Aplicando la regla del producto, hay

$$ \dbinom{13}{1}\cdot\dbinom{4}{3}\cdot\dbinom{12}{1}\cdot\dbinom{4}{2} = 13\cdot4\cdot12\cdot6 = 3744 $$

manos que son full.

Finalmente, en el apartado (e), de los $13$ números disponibles en la baraja seleccionamos dos de ellos ($C_{13,2}$), de los cuales, de entre las cuatro cartas asociadas a cada uno de ellos, escogeremos dos idénticas ($C_{4,2}\cdot C_{4,2}$). Por último, de las restantes cartas, $52-4-4=44$, tomaremos una de ellas cualquiera ($C_{44,1}$). Aplicando la regla del producto hay

$$ \dbinom{13}{2}\cdot\dbinom{4}{2}\cdot\dbinom{4}{2}\cdot\dbinom{44}{1} = 78\cdot6\cdot6\cdot44 = 123552 $$

manos que son doble pareja.

Problema 3

• (a) ¿Cuántas fichas tiene el dominó?
• (b) Tenemos siete urnas indistinguibles entre sí y dos bolas idénticas, ¿de cuántas formas se pueden meter las bolas en las urnas?
• (c) Calcula el número de soluciones enteras no negativas de la ecuación $x_1+x_2+\cdots+x_7=2$.

Solución: para el apartado (a), en las fichas del dominó encontramos representados los números desde el $0$ (blanca) al $6$, que aparecen de dos en dos. Por ejemplo, son fichas de este juego los pares $(1,2)$ o $(6,0)$. Por otro lado, el orden en que escojamos los números para conformar una ficha no importa, pues, por ejemplo, los pares $(1,2)$ y $(2,1)$ representan una única ficha del dominó. Finalmente, el juego incorpora fichas en la que se repiten los elementos, como $(0,0)$ o $(5,5)$, por nombrar algunas. Por tanto, estamos interesados en el total de combinaciones con repetición de siete elementos tomados de dos en eso y, entonces, hay

$$ CR_{7,2} = \dbinom{7+2-1}{2} = \dbinom{8}{2} = \dfrac{8\cdot7}{2} = 28 $$

fichas en el juego del dominó.

A continuación, en el apartado (b), si representamos gráficamente nuestras siete urnas indistinguibles como sigue

$$ (\ \ |\ \ |\ \ |\ \ |\ \ |\ \ |\ \ ), $$

esto es, como si pusiéramos seis rayas sobre la recta real y representamos las bolas como $*$, una posible configuración sería

$$ (\ \ | * |\ \ | * |\ \ |\ \ |\ \ ). $$

No obstante, si ahora movemos la última raya al principio, la anterior configuración se convierte en

$$ (\ \ |\ \ | * |\ \ | * |\ \ |\ \ ). $$

Así pues, observamos que, de cara a contar posibilidades en este apartado, es como si tuviéramos ocho elementos (las dos bolas, $*$, y las seis rayas, $|$) de dos tipos. Uno de ellos se repite dos veces (las bolas), mientras que el otro se repite en seis ocasiones (las rayas). Por tanto, hay

$$ PR_{8}^{2,6} = \dfrac{8!}{2!\cdot6!} = \dfrac{8\cdot7}{2}=28 $$

formas de introducir dos bolas idénticas en siete urnas indistinguibles entre sí.

Finalmente, para el apartado (c ), de cara a encontrar las soluciones enteras no negativas de la ecuación $x_1+x_2+\cdots+x_7=2$, observamos rápidamente que cada variable puede tomar, como máximo, los valores $0$, $1$ o $2$. Así pues, podemos representar la situación como hicimos en el apartado anterior, donde ahora cada ‘‘urna’’ sería cierta variable $x_i$, con $i=1,2,\ldots,7$, y el valor de dicha variable vendría dado por el número de ‘‘bolas’’ que tuviese en su interior (para un $i$ dado, con $0$ bolas, $x_i=0$; con $1$ bola, $x_i=1$; y con $2$ bolas, $x_i=2$). Por tanto, razonando como antes, la ecuación dada posee

$$ PR_{8}^{2,6} = \dfrac{8!}{2!\cdot6!} = \dfrac{8\cdot7}{2}=28 $$

soluciones enteras no negativas.

Por otro lado, si recordamos de ejercicios anteriores, podemos utilizar las combinaciones con repetición como herramienta para contar el número de bolas idénticas que introducimos en urnas indistinguibles entre sí. Considerando esto, el presente ejercicio se reduce a calcular $CR_{7,2}$. En resumen,

• hallar el número de soluciones de la ecuación $x_1+x_2+\cdots+x_n=r$, con $x_i\geq 0$ para $1\leq i\leq n$ y $r$ entero no negativo,
• encontrar el número de maneras de seleccionar una muestra de tamaño $r$, con elementos repetidos o no, de una colección de tamaño $n$, y
• calcular el número de formas de distribuir $r$ objetos idénticos entre $n$ destinatarios distintos

es lo mismo.

Problema 4

Calcula el número de soluciones enteras de la ecuación

$$ x_1+x_2+\cdots+x_8=24, $$

donde $x_i\geq 2$, para $1\leq i\leq 8$.

Solución: a diferencia del ejercicio anterior, aquí no buscamos hallar el total de soluciones enteras no negativas de la ecuación, pues nos indican que $x_i\geq 2$, para todo $1\leq i\leq 8$. No obstante, podemos razonar de la siguiente forma: asumamos que disponemos de ocho urnas indistinguibles entre sí y almacenemos dos bolas en cada una de ellas para empezar. De esta manera, quedarán $24 - 2\cdot8 = 8$ bolas idénticas por introducir en las urnas, acción que podemos llevar a cabo de

$$ PR_{15}^{8,7} = \dfrac{15!}{8!\cdot 7!} = \dfrac{15\cdot14\cdot13\cdot12\cdot11\cdot10\cdot9}{7!} = 6435 $$

maneras posibles. A este resultado hemos arribado, recordemos, dado que son necesarias siete barras, para representar las ocho urnas sobre la recta real, y hemos de almacenar ocho estrellas en los huecos que dicha configuración produce. Así pues, son $6435$ el número de soluciones enteras para la ecuación planteada, considerando que $x_i\geq 2$, para todo $1\leq i\leq 8$.

Si nos damos cuenta, simplemente hemos ignorado aquella parte del problema que sabemos está fija. Técnicamente, esta acción es equivalente a llevar a cabo un cambio de variable del tipo

$$ x_i = x^{\prime}_i + 2, $$

para $1\leq i\leq 8$, que transforma la ecuación inicial planteada en

$$ (x^{\prime}_1 + 2) + (x^{\prime}_2 + 2) + \cdots + (x^{\prime}_8+2) = 24, $$

que es equivalente a $x^{\prime}_1 +x^{\prime}_2 +\cdots+x^{\prime}_8 =8$, con la salvedad de que ahora $x^{\prime}_i\geq 0$, para todo $1\leq i\leq 8$ y entonces ahora basta con aplicar los métodos que utilizamos en ejercicios anteriores.

Problema 5

¿Cuántos números entre $1$ y $600$ no son divisibles por $3$, ni por $5$, ni por $7$?

Solución: emplearemos el Principio de inclusión-exclusión para resolver el presente problema. Así, definamos los conjuntos

• $3$ como ‘‘conjunto de números menores o iguales que $600$ que son divisibles por $3$’’,
• $5$ como ‘‘conjunto de números menores o iguales que $600$ que son divisibles por $5$’’, y
• $7$ como ‘‘conjunto de números menores o iguales que $600$ que son divisibles por $7$’’.

Estamos interesados en el cardinal del conjunto de números que, precisamente, no son divisibles por $3$, ni por $5$, ni por $7$, esto es, $card(\overline{3}\cap\overline{5}\cap\overline{7})$ . Ahora bien, por las Leyes de DeMorgan, trabajaremos con el suceso complementario, ya que es más fácil contar múltiplos que números que no son múltiplos,

$$ card(\overline{3}\cap\overline{5}\cap\overline{7}) = card(\overline{3\cup 5\cup 7}) = card(E) - card(3\cup 5\cup 7), $$

donde por $E$ representamos el conjunto de los números enteros positivos menores o iguales que $600$, es decir, el conjunto total, cuyo cardinal asciende, en esta ocasión concreta, a $600$. Por tanto,

$$ card(\overline{3}\cap\overline{5}\cap\overline{7}) = 600 - card(3\cup 5\cup 7). $$

A continuación, por el Principio de inclusión-exclusión,

$$ \begin{aligned} card(3\cup 5\cup 7) &= card(3) + card(5) + card(7)\\ &\quad -card(3\cap 5) - card(3\cap 7) - card(5\cap 7)\\ &\quad +card(3\cap 5\cap 7), \end{aligned} $$

donde

• $card(3)$ representa el total de múltiplos de $3$ menores o iguales que $600$, esto es,

$$ card(3) = \left\lfloor\dfrac{600}{3}\right\rfloor=200. $$

• $card(5)$ representa el total de múltiplos de $5$ menores o iguales que $600$, esto es,

$$ card(5) = \left\lfloor\dfrac{600}{5}\right\rfloor=120. $$

• $card(7)$ representa el total de múltiplos de $7$ menores o iguales que $600$, esto es,

$$ card(7) = \left\lfloor\dfrac{600}{7}\right\rfloor=85. $$

• $card(3\cap 5)$ representa el total de múltiplos de $3$ y de $5$ menores o iguales que $600$, esto es,

$$ card(3\cap 5) = \left\lfloor\dfrac{600}{3\cdot 5}\right\rfloor=40. $$

• $card(3\cap 7)$ representa el total de múltiplos de $3$ y de $7$ menores o iguales que $600$, esto es,

$$ card(3\cap 7) = \left\lfloor\dfrac{600}{3\cdot 7}\right\rfloor=28. $$

• $card(5\cap 7)$ representa el total de múltiplos de $5$ y de $7$ menores o iguales que $600$, esto es,

$$ card(5\cap 7) = \left\lfloor\dfrac{600}{5\cdot 7}\right\rfloor=17. $$

• $card(3\cap 5\cap 7)$ representa el total de múltiplos de $3$, de $5$ y de $7$ menores o iguales que $600$, esto es,

$$ card(3\cap 5\cap 7) = \left\lfloor\dfrac{600}{3\cdot 5\cdot 7}\right\rfloor=5. $$

Por consiguiente,

$$ card(\overline{3}\cap\overline{5}\cap\overline{7}) = 600 - (200 + 120 + 85 - 40 - 28 - 17 + 5) = 275, $$

es decir, hay $275$ números entre $1$ y $600$, ambos inclusive, que no son divisibles por $3$, ni por $5$, ni por $7$.

Problema 6

• (a) Demuestra que escogidos siete números enteros al azar, la diferencia entre dos de ellos es múltiplo de seis.
• (b) Demuestra que todo número entero $n$ tiene un múltiplo cuya expresión decimal está compuesta por ceros y unos.

Solución: para el apartado (a), empecemos considerando un ejemplo concreto: sean los números enteros, escogidos al azar, $53$, $75$, $32$, $7$, $83$, $1$ y $10$. Si obtenemos el valor de la congruencia de cada uno de ellos módulo seis, es cierto que

$$ \begin{aligned} 53&\equiv 5\pmod{6},\\ 75&\equiv 3\pmod{6},\\ 32&\equiv 2\pmod{6},\\ 7&\equiv 1\pmod{6},\\ 83&\equiv 5\pmod{6},\\ 1&\equiv 1\pmod{6},\\ 10&\equiv 4\pmod{6}. \end{aligned} $$

Basta ahora tomar dos cuyo valor de la congruencia módulo seis coincida para encontrar un múltiplo de seis. Efectivamente, por ejemplo,

$$ 83-53=30 = 6\cdot5. $$

En general, como el menor sistema completo de restos módulo $6$ está conformado por seis valores, $\{0,1,2,3,4,5\}$, dados siete números escogidos al azar sabemos, por el Principio del palomar, que al menos dos de ellos poseerán el mismo valor de la congruencia módulo seis. Esto es, existen al menos $x, y\in\mathbb{Z}$ tal que $x\equiv a\pmod{6}$ e $y\equiv a\pmod{6}$, con $a\in\{0,1,2,3,4,5\}$. Por consiguiente,

$$ (x-y)\equiv (a-a)\pmod{6}\equiv 0\pmod{6}, $$

es decir, la diferencia es múltiplo de seis.

Para el apartado (b) utilizaremos la misma estrategia, pero escogiendo los números con cautela, ya que buscamos que el múltiplo que nos interesa únicamente posea en su expresión decimal ceros y unos. Como antes, empecemos considerando un ejemplo concreto: sea $n=6$. Trabajemos pues con el conjunto de siete números

$$ \{1,11,111,1111,11111,111111,1111111\}, $$

para el que, por el Principio del palomar, sabemos que al menos dos de ellos poseerán el mismo valor de su congruencia módulo seis. Efectivamente,

$$ 1\equiv 1\pmod{6}\qquad\text{y}\qquad 1111\equiv 1\pmod{6}. $$

Así, $(1111 - 1)\equiv 0\pmod{6}$, esto es, $1110 = 6\cdot185$ es múltiplo de $6$ y en su expresión decimal únicamente aparecen ceros y unos.

En general, dado un número natural $n$, consideramos el conjunto

$$ \{1,11,111,1111,\ldots\} $$

de $n+1$ elementos. Por el Principio del palomar, al menos dos de dichos elementos poseerán el mismo valor de su congruencia módulo $n$. Designemos por $a$ y $b$ a tales elementos que verifican $a\equiv x\pmod{n}$ y $b\equiv x\pmod{n}$, entonces $(a-b)\equiv 0\pmod{n}$, esto es, la diferencia entre ellos es múltiplo de $n$, y, por tal y como hemos construido el anterior conjunto, su expresión únicamente poseerá ceros y unos.

A modo anecdótico, si en el problema nos hubiesen solicitado demostrar que todo número entero $n$ tiene un múltiplo cuya expresión decimal está compuesta por ceros y doses, habría bastado considerar un conjunto del tipo

$$ \{2,22,222,2222,\ldots\}. $$

Variantes similares del problema únicamente exigen encontrar un conjunto adecuado al que aplicar la estrategia esbozada en párrafos anteriores.

Problema 7

¿Cuántos términos tiene la expansión de $(x_1+x_2+\cdots+x_s)^n$?

Solución: empecemos estudiando algunos casos sencillos para comprobar si podemos inferir algún patrón de comportamiento. Por ejemplo, sabemos que

$$ (x+y)^2 = x^2 + y^2 + xy, $$

es decir, la expansión de $(x+y)^2$ posee tres términos. Análogamente,

$$ (x+y)^3 = x^3 + 3x^2 y + 3xy^2 + y^3, $$

esto es, la expansión de $(x+y)^3$ posee cuatro términos. En general, por el Teorema del binomio,

$$ (x+y)^n = \dbinom{n}{0}x^n y^0 + \dbinom{n}{1}x^{n-1} y^1+\cdots+\dbinom{n}{n}x^0 y^n. $$

Rápidamente observamos que cada uno de los sumandos del anterior desarrollo posee una peculiar característica: la suma de las potencias de $x$ e $y$ asciende a $n$, el grado del binomio. Esto es cierto asimismo para los dos primeros ejemplos que consideramos arriba, sin más que escribirlos de la siguiente manera para que quede patente,

$$ \begin{aligned} (x+y)^2 &= x^2 y^0 + y^2 x^0 + x^1 y^1,\\ (x+y)^3 &= x^3 y^0 + 3x^2 y^1 + 3x^1 y^2 + y^3 x^0. \end{aligned} $$

Así pues, estamos interesados en saber de cuántas maneras podemos repartir el grado entre las variables involucradas en el desarrollo. En los ejemplos anteriores, $x$ e $y$ jugarían el papel de dos urnas indistinguibles, mientras que el grado $n$ adoptaría el rol de las $n$ bolas idénticas. Utilizando la estrategia de barras y estrellas, necesitamos una barra para representar sobre la recta real las dos urnas y buscamos ubicar luego $n$ estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de términos en la expansión de un binomio de grado $n$, equivale a la cantidad de permutaciones con repetición de $n+1$ elementos, donde uno de ellos se repite una vez, mientras que el otro lo hace en $n$ ocasiones. Así, hay

$$ PR_{n+1}^{1,n} = \dfrac{(n+1)!}{1!\cdot n!} = n+1 $$

términos en el desarrollo de un binomio de grado $n$.

Por otro lado,

$$ (x+y+z)^2 = x^2 +y^2 +z^2 +2xy+2xz+2yz, $$

esto es, el desarrollo de $(x+y+z)^2$ posee seis términos. Si lo escribimos como

$$ \begin{aligned} (x+y+z)^2 &= x^2 y^0 z^0 + x^0 y^2 z^0 + x^0 y^0 z^2\\ &\quad + 2x^1 y^1 z^0 + 2x^1 y^0 z^1 + 2x^0 y^1 z^1, \end{aligned} $$

rápidamente apreciamos que estamos repartiendo el grado, $2$, en tres urnas indistinguibles, $x$, $y$ y $z$. Aplicando, como antes, la estrategia de barras y estrellas, dicha acción la podemos llevar a cabo de

$$ PR_{2+2}^{2,2} = PR_{4}^{2,2} = \dfrac{4!}{2!\cdot 2!} = 6 $$

formas posibles.

En general, para la expresión $(x_1+x_2+\cdots+x_s)^n$ vamos a considerar que disponemos de $s$ urnas indistinguibles, las respectivas variables $x_1,x_2,\ldots,x_s$. En ellas buscamos repartir $n$ bolas idénticas, el grado $n$. Utilizando la estrategia de barras y estrellas, necesitamos $s-1$ barras para representar sobre la recta real las $s$ urnas y buscamos ubicar luego $n$ estrellas en los huecos que dicha configuración produce. Por tanto, el número de términos del desarrollo de $(x_1+x_2+\cdots+x_s)^n$, equivale a la cantidad de permutaciones con repetición de $s-1+n$ elementos, donde uno de ellos se repite $s-1$ veces, mientras que el otro hace en $n$ ocasiones. Así, hay

$$ PR_{s-1+n}^{s-1,n} = \dfrac{(n+s-1)!}{n!(s-1)!} $$

términos en el desarrollo de $(x_1+x_2+\cdots+x_s)^n$.

Problema 8

¿De cuántas maneras pueden cinco chicos y tres chicas sentarse alrededor de una mesa si

• (a) no hay restricción alguna?
• (b) el chico $H_1$ y la chica $M_1$ no pueden estar juntos?
• (c) ninguna chica ha de tener a otra a su lado?

Solución: para el apartado (a), al no imponer restricción alguna sobre la disposición de los ocho integrantes del grupo, el número de formas en las que pueden sentarse alrededor de una mesa equivale al total de permutaciones circulares de ocho elementos. Así, tienen

$$ PC_8 = (8-1)! = 7! = 5040 $$

maneras de sentarse alrededor de la mesa.

Por lo que respecta al apartado (b), ya que acabamos de calcular en el párrafo anterior el total de maneras en que pueden sentarse, resulta más sencillo utilizar ahora el Principio de complementación, que recordemos dice si $A$ es un subconjunto de un conjunto finito universal $U$, entonces

$$ card(U - A) = card(U) - card(A). $$

De esta forma, en lugar de contar el número de formas en que $H_1$ y $M_1$ pueden sentarse estando separados (es decir, con al menos un integrante del grupo entre ellos), averigüemos de cuántas maneras pueden sentarse todos alrededor de la mesa estando $H_1$ y $M_1$ juntos. Así, si consideramos la pareja como una unidad, el nuevo problema se reduce a encontrar el número de formas en que pueden disponerse siete elementos alrededor de una mesa, que sabemos equivale al total de permutaciones circulares de siete elementos, esto es,

$$ PC_7 = (7-1)! = 6! = 720. $$

Ahora bien, como la pareja puede sentarse de maneras posibles, ($H_1M_1$ y $M_1H_1$), hemos de incorporar las permutaciones de dos elementos ($2! = 2$) al anterior resultado, aplicando la regla del producto. Por consiguiente, existen $720\cdot2 = 1440$ formas de sentarse los ocho integrantes del grupo asumiendo que $H_1$ y $M_1$ se colocaron uno al lado del otro. Luego, por el Principio de complementación hay

$$ 7! - 1440 = 3600 $$

maneras de disponer a los miembros del grupo donde $H_1$ y $M_1$ no están juntos.

Finalmente, en el apartado (c), comencemos sentando a los chicos en la tabla, ya que su número es más elevado que el de chicas. Por apartados anteriores, sabemos que el número de formas de sentar cinco personas alrededor de una tabla asciende al total de permutaciones circulares de cinco elementos, esto es,

$$ PC_5 = (5-1)! = 4! = 24 $$

maneras posibles. A continuación, en los huecos que quedan entre ellos, empecemos a sentar chicas. Para la primera de ella encontramos cinco opciones disponibles, pues tal es el número de huecos que quedan entre los chicos. Para la segunda chica, una vez sentada la primera, dichas opciones se reducen a cuatro. Por último, la tercera chica, una vez sentadas las otras dos, puede escoger entre las tres posiciones disponibles que restan. Luego, aplicando la regla del producto hay

$$ 4! \cdot 5\cdot 4\cdot3 = 1440 $$

maneras de disponer a los ocho integrantes del grupo de forma que ninguna chica tenga a otra a su lado.

Problema 9

Encuentra el número de maneras en que pueden sentarse $n$ matrimonios alrededor de una mesa si

• (a) hombres y mujeres se alternan.
• (b) cada mujer está sentada al lado de su marido.

Solución: para el apartado (a) empecemos sentando, por ejemplo, a los hombres (podríamos haber iniciado la resolución colocando a las mujeres asimismo, pues el número de personas coincide). Sabemos, por ejercicios anteriores, que el total de formas de sentar a $n$ personas alrededor de una mesa asciende al total de permutaciones circulares de $n$ elementos, esto es, hay

$$ PC_n = (n-1)! $$

maneras. A continuación, comencemos a sentar mujeres. La primera de ellas puede hacerlo en cualesquiera de los $n$ huecos que la configuración de los hombres produce. Para la segunda, una vez sentada la primera, son $n-1$ las opciones que tiene a su disposición para ubicarse. En cuanto a la tercera, una vez sentadas las dos anteriores, tiene a su disposición $n-2$ asientos para escoger su sitio, y así sucesivamente. Aplicando la regla del producto, hay

$$ (n-1)!\cdot n\cdot(n-1)\cdot(n-2)\cdot\ldots\cdot2\cdot1 = (n-1)!n! $$

maneras en que pueden sentarse $n$ matrimonios alrededor de una mesa si hombres y mujeres han de alternar sus sitios.

Para el apartado (b), consideremos cada matrimonio como una unidad indivisible. Sabemos, por ejercicios anteriores, que el número de formas de disponer $n$ elementos alrededor de una mesa equivale al total de permutaciones circulares de $n$ elementos, es decir, $PC_n = (n-1)!$. Ahora bien, el primer matrimonio puede sentarse de dos maneras posibles (hombre - mujer o mujer - hombre), hecho que hemos de tener en cuenta. Lo mismo sucede para el segundo matrimonio, para el tercero, y así sucesivamente. Por consiguiente, aplicando la regla del producto, existen

$$ (n-1)!\cdot2\cdot2\cdot\ldots\cdot2 = (n-1)!\cdot2^n $$

maneras en que pueden sentarse $n$ matrimonios alrededor de una mesa si cada mujer ha de estar sentada al lado de su marido. Alternativamente, podemos abordar este apartado sentando primero a los hombres, acción que sabemos podemos llevar a cabo de $PC_n=(n-1)!$ formas posibles y luego considerar que cada mujer tiene sus opciones bastante limitadas a la hora de sentarse, pues únicamente puede hacerlo de dos manera posibles (a la izquierda o a la derecha de su marido). Como hemos de colocar $n$ mujeres asumiendo la restricción anterior, son $2^n$ las formas posibles y aplicando la regla del producto se llega al resultado alcanzado arriba.

Problema 10

En un puesto de mando, para transmitir señales, hay en línea recta cuatro astas. En cada asta solamente se puede colocar una bandera. Las señales consisten en colocar banderas de distintos colores en dichas astas. Según el número de banderas colocadas, colores de las mismas y lugar que ocupen, la señal será distinta. Halla el número de señales que se pueden transmitir si se posee un juego de siete banderas con los colores del arco iris.

Solución: una de las claves de este ejercicio pasa por darse cuenta de que en cada asta se ‘‘puede’’ colocar (o no) una bandera para transmitir una determinada señal. Así pues, hemos de discutir las opciones posibles, para las señales disponibles, en función del número de astas empleadas:

• Si emplean las cuatro astas, dado que el orden en el que coloquen las banderas importa y no es posible repetir bandera alguna, la cantidad de señales que pueden transmitir en este caso equivale al número de variaciones de siete elementos tomados de cuatro en cuatro, esto es,

$$ V_{7,4} = 7\cdot6\cdot5\cdot4 = 840. $$

• Si utilizan tres astas, ello implica que de las cuatro disponibles han de escoger tres, acción que pueden llevar a cabo de $C_{4,3}$ maneras posibles. Una vez escogidas las astas, como el orden en el que coloquen las banderas importa y no pueden repetir bandera alguna, podrían transmitir, para una elección de astas particular, un total de señales que asciende al número de variaciones de siete elementos tomados de tres en tres, es decir, $V_{7,3}$. Ahora, aplicando la regla del producto, utilizando tres astas pueden transmitir un número de señales que asciende a

$$ C_{4,3}\cdot V_{7,3} = \dbinom{4}{3}\cdot7\cdot6\cdot5 = 840. $$

• Si utilizan dos astas, ello implica que de las cuatro disponibles han de escoger dos, acción que pueden llevar a cabo de $C_{4,2}$ maneras posibles (aquí, como antes, no importa el orden, pues es igual escoger las astas primera y segunda, que las astas segunda y primera, lo importante ahora es seleccionar dos astas). Una vez escogidas las astas, como el orden en el que coloquen las banderas importa y no pueden repetir bandera alguna, podrían transmitir, para una elección de astas particular, un total de señales que asciende al número de variaciones de siete elementos tomados de dos en dos, es decir, $V_{7,2}$. Ahora, aplicando la regla del producto, utilizando dos astas pueden transmitir un número de señales que asciende a

$$ C_{4,2}\cdot V_{7,2} = \dbinom{4}{2}\cdot7\cdot6 = 252. $$

• Si utilizan una asta, ello implica que de las cuatro disponibles han de escoger una, acción que pueden llevar a cabo de cuatro maneras posibles. Una vez escogida, tienen siete opciones de cara a escoger la bandera que emplearán para transmitir la señal. Ahora, aplicando la regla del producto, utilizando una asta pueden transmitir un número de señales que asciende a

$$ C_{4,1}\cdot V_{7,1} = 4\cdot7 = 28. $$

• Finalmente, existe una posibilidad adicional que hemos de considerar y consiste en que no utilicen bandera alguna para transmitir una determinada señal (esto es, que no hagan uso de ninguna asta).

Recapitulando, si se posee un juego de siete banderas con los colores del arco iris y cuatro astas donde colocarlas, podrán transmitir un total de

$$ 840+840+252+28+1 = 1961 $$

señales.

Problema 11

Obtén el número de diagonales que se pueden trazar en un cuadrado, en un hexágono y en un polígono de $n$ lados. ¿Existe algún polígono tal que el número de lados coincide con el número de diagonales?

Solución: a la vista de la figura siguiente, por recuento, concluimos que un cuadrado posee dos diagonales, mientras que en un hexágono el número de diagonales asciende a nueve.

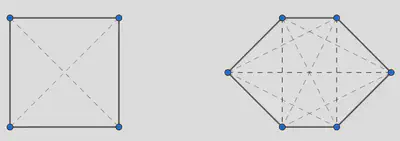
En general, para poder dibujar una diagonal necesitamos unir dos de los vértices del correspondiente polígono, por lo que hemos de ser capaces de averiguar el número de formas en que podemos seleccionar los mencionados dos vértices. Como no importa el orden en el que los escojamos, el total equivale a la cantidad de combinaciones de $n$ elementos tomados de dos en dos, esto es, a $C_{n,2}$. No obstante, hemos de actuar con cautela, puesto que, de la manera indicada, estaríamos considerando como diagonal también la unión de dos vértices contiguos, es decir, cada uno de los lados. Así pues, sustrayendo estos, la cantidad de diagonales de un polígono de $n$ lados asciende a

$$ C_{n,2} - n = \dbinom{n}{2} - n = \dfrac{n(n-1)}{2} - n = \dfrac{n^2-n-2n}{2} = \dfrac{n^2-3n}{2}. $$

Alternativamente, fijado un vértice del polígono de $n$ lados, generamos diagonales si lo unimos con los vértices que no le son contiguos, es decir, con los restantes $n-3$ vértices. Así, cada vértice posee asociadas $n-3$ diagonales. Como contamos con $n$ vértices, aplicando la regla del producto, hablaríamos de un total de $n(n-3)$ diagonales. Sin embargo, procediendo así, debemos pensar que cada diagonal se cuenta en dos ocasiones, de manera que, corrigiendo por dicho factor, el total de diagonales de un polígono de $n$ lados es

$$ \dfrac{n(n-3)}{2} = \dfrac{n^2 -3n}{2} $$

como antes.

Ahora, para dar respuesta a la pregunta planteada en el enunciado del ejercicio, igualando el total de diagonales de un polígono de $n$ lados con su número de lados, tenemos

$$ \dfrac{n^2 -3n}{2} = n. $$

Es decir, se conforma la ecuación $n^2 -3n=2n$ o, equivalentemente, $n^2 -5n=0$. Esta posee dos soluciones, la trivial, $n=0$, que rechazamos por no conformar un polígono propiamente dicho; y $n=5$, esto es, el pentágono es el único polígono cuyo número de lados coincide con su cantidad de diagonales.

Problema 12

Suben dos mujeres y tres hombres a un ascensor en la planta baja de un edificio de seis pisos. Averigua de cuántas maneras se pueden bajar del ascensor, sabiendo que en un mismo piso no pueden bajar personas de distinto sexo.

Solución: en adelante, vamos a considerar que un edificio de seis pisos posee cinco plantas a las que subir en ascensor, esto es, contaremos la planta baja como un piso más y, obviamente, para acceder a ella no necesitamos utilizar el ascensor.

En primer lugar, asumamos que las mujeres son indistinguibles, así como los hombres, pues parece la interpretación más natural tras una primera lectura del enunciado. Empezaremos organizando la bajada de ellas, pues son menos personas a considerar y únicamente encontramos dos opciones posibles: que bajen juntas o por separado.

Si ambas bajan juntas en un mismo piso, son cinco las opciones que se les presentan disponibles, desde la planta primera hasta la quinta. A continuación, por lo que respecta a los hombres, cuatro son las plantas que les quedan para bajar los tres. Pueden hacerlo los tres juntos en una misma planta, cada uno por separado en plantas distintas, dos en una misma planta y el tercero en otra diferente, y así sucesivamente. Enseguida apreciamos que el problema es equivalente a uno de los tratados anteriormente: disponer sobre urnas indistinguibles cierto número de bolas idénticas.

En esta ocasión, las cuatro plantas restantes harían el papel de urnas, mientras que los tres hombres adoptarían el rol de bolas. Utilizando la estrategia de barras y estrellas, necesitamos tres barras para representar sobre la recta real las cuatro urnas y buscamos ubicar luego tres estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que pueden bajar los tres hombres del ascensor, en las cuatro plantas restantes, equivale a la cantidad de permutaciones con repetición de seis elementos, donde cada uno de ellos se repite en tres ocasiones, esto es,

$$ PR_{6}^{3,3} = CR_{4,3} = \dbinom{4+3-1}{3} = \dbinom{6}{3} = 20. $$

Así, aplicando la regla del producto, cuando las dos mujeres bajan juntas, las cinco personas pueden bajar del ascensor de $5\cdot20=100$ maneras posibles.

A continuación, asumamos que las mujeres bajan cada una en una planta diferente. Como hemos supuesto que ambas son indistinguibles, esta acción la pueden realizar de tantas formas como número de combinaciones de cinco elementos tomados de dos en dos hay (puesto que el orden no importa, es indiferente que una baje en el primero y otra en el tercero o en el orden contrario), es decir,

$$ C_{5,2} = \dbinom{5}{2} = 10. $$

Así, ahora quedan tres pisos disponibles para que bajen los tres hombres. Por un razonamiento similar al llevado a cabo arriba, el problema sería equivalente al de almacenar tres bolas idénticas en tres urnas indistinguibles. Utilizando la estrategia de barras y estrellas, necesitamos dos barras para representar sobre la recta real las tres urnas y buscamos ubicar luego tres estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que pueden bajar del ascensor los tres hombres, en las tres plantas restantes, equivale a la cantidad de permutaciones con repetición de cinco elementos, donde uno de ellos se repite en tres ocasiones, mientras que el otro lo hace dos veces, esto es,

$$ PR_{5}^{3,2} = CR_{3,3} = \dbinom{3+3-1}{3} = \dbinom{5}{3} = 10. $$

Así, aplicando la regla del producto, cuando las dos mujeres bajan por separado, las cinco personas pueden bajar del ascensor de $10\cdot10=100$ maneras posibles.

Finalmente, por el principio de adición, son $100+100=200$ las maneras en que dos mujeres y tres hombres pueden bajar del ascensor, en un edificio de seis pisos, sabiendo que en un mismo piso no pueden bajar personas de distinto sexo.

En segundo lugar, consideremos que las cinco personas son distinguibles (que sería el caso, por ejemplo, de que nos las hubiesen presentado cada una por su nombre). Actuaremos de forma similar a como hicimos en los párrafos anteriores, empezando por estudiar las formas en las que pueden bajar las mujeres: juntas o separadas.

Si bajan juntas, como antes, son cinco las opciones que se les presentan disponibles, una por cada una de las cinco plantas. Ahora, por lo que respecta a los hombres, les quedan cuatro plantas donde poder bajar del ascensor. Como el orden en esta ocasión sí es importante y en una misma planta pueden bajar varios de ellos, el número de maneras en que pueden bajar equivale a la cantidad de variaciones con repetición de cuatro elementos tomados de tres en tres, esto es, $VR_{4,3} = 4^3 = 256$. Aplicando la regla del producto, cuando las dos mujeres bajan juntas, las cinco personas pueden bajar del ascensor de $5\cdot256 = 1280$ maneras posibles.

Si las mujeres bajan por separado, dado que importa el orden en el que lo hagan, la cantidad de formas en que pueden hacerlo asciende al total de variaciones de cinco elementos tomadas de dos en dos, es decir, $V_{5,2} = 5\cdot4 = 20$. Ahora, por lo que respecta a los hombres, les quedan tres plantas donde poder bajar del ascensor. Como el orden en esta ocasión sí es importante y en una misma planta pueden bajar varios de ellos, el número de maneras en que pueden bajar equivale a la cantidad de variaciones con repetición de tres elementos tomados de tres en tres, esto es, $VR_{3,3} = 3^3 = 27$. Aplicando la regla del producto, cuando las dos mujeres bajan juntas, las cinco personas pueden bajar del ascensor de $20\cdot27 = 540$ maneras posibles.

Finalmente, por el principio de adición, son $1280+540=1820$ las maneras en que dos mujeres y tres hombres (todos ellos distinguibles) pueden bajar del ascensor, en un edificio de seis pisos, sabiendo que en un mismo piso no pueden bajar personas de distinto sexo.

Nota: si interpretamos el enunciado asignando seis plantas al edificio, habremos de llevar a cabo las oportunas correcciones en el argumento expuesto.

Problema 13

Un desarreglo es una permutación de objetos en la que ningún objeto está en su posición original. Por ejemplo, $234561$ es un desarreglo de $123456$, pero $213645$ no, ya que $3$ está en su posición original.

• (a) Escribe los desarreglos de $123$.
• (b) Demuestra que, dados $n$ objetos, el total de desarreglos asciende a

$$ D_n = n!\left(1-\dfrac{1}{1!} + \dfrac{1}{2!} - \dfrac{1}{3!}+\cdots+(-1)^n \dfrac{1}{n!}\right). $$

Solución: en cuanto al apartado (a), empecemos escribiendo todas las permutaciones de $123$,

$$ 123,\quad 132,\quad 213,\quad 231,\quad 312,\quad 321. $$

De entre ellas, descartamos $123$ y $132$, por mantener $1$ su posición original; asimismo hacemos lo propio con $321$, porque $2$ permanece invariante; y con $213$, ya que $3$ continúa en el mismo lugar. Por tanto, dos son los desarreglos de $123$, a saber, $231$ y $312$.

Para abordar el apartado (b) haremos uso del Principio de complementación, y, en lugar de buscar la cantidad de desarreglos, hallaremos el número de permutaciones que al menos mantienen una cifra en su posición original (los ‘‘arreglos’’), pues, aunque resulte sorprendente a primera vista, es más fácil contar estas últimas. Una vez encontrado dicho número, se lo sustraeremos al total de permutaciones, obteniendo así la cifra de desarreglos.

Por consiguiente, para empezar, dados $n$ objetos, sabemos que el total de permutaciones posibles asciende a $P_n = n!$. Ahora, definamos $A_i$ como el total de conjuntos en el que $i$ objetos mantienen su posición original, con $1\leq i\leq n$. Por tanto, el número de desarreglos vendrá dado por

$$ D_n = n! - card(A_1\cup A_2\cup\cdots\cup A_n). $$

Ahora bien, ¿cuántos conjuntos encontramos que se caractericen por mantener un objeto su posición original? De entre los $n$ objetos, seleccionamos uno, acción que podemos llevar a cabo de $C_{n,1}$ maneras posibles. Después, el resto de objetos, $n-1$, simplemente los permutamos, situación que podemos realizar de $P_{n-1} = (n-1)!$ formas posibles. Aplicando la regla del producto hay

$$ C_{n,1}(n-1)! = \dbinom{n}{1}(n-1)! $$

conjuntos que mantienen un objeto en su posición original. Análogamente, ¿cuántos conjuntos encontramos que se caractericen por mantener dos objetos sus posiciones originales? De entre los $n$ objetos, seleccionamos dos, acción que podemos llevar a cabo de $C_{n,2}$ maneras posibles. Luego, el resto de objetos, $n-2$, simplemente los permutamos, situación que podemos realizar de $P_{n-2} = (n-2)!$ formas posibles. Aplicando la regla del producto hay

$$ C_{n,2}(n-2)! = \dbinom{n}{2}(n-2)! $$

conjuntos que mantienen dos objetos en sus posiciones originales. El mismo razonamiento se puede aplicar para el caso de tres objetos, cuatro objetos, etc.

Por consiguiente, aplicando el Principio de inclusión-exclusión,

$$ \begin{aligned} D_n &= n! - card(A_1\cup A_2\cup\cdots\cup A_n)\\ &= n!-\left(\dbinom{n}{1}(n-1)! - \dbinom{n}{2}(n-2)! + \cdots + (-1)^{n+1} \dbinom{n}{n}\right)\\ &= n! - \left(\dfrac{n}{1}\cdot(n-1)! - \dfrac{n(n-1)}{2}\cdot(n-2)! + \cdots + (-1)^{n+1} \cdot 1\right)\\ &= n! - \left(\dfrac{n!}{1} - \dfrac{n!}{2} + \cdots + (-1)^{n+1} \dfrac{n!}{n!}\right)\\ &= n!\left(1 - \dfrac{1}{1!} + \dfrac{1}{2!} - \cdots + (-1)^n \dfrac{1}{n!}\right), \end{aligned} $$

tal y como queríamos demostrar.

Problema 14

En una fiesta, a la que acuden seis chicos y seis chicas, comienza a sonar la primera canción,

• (a) ¿de cuantas formas pueden organizarse para bailar todos ellos por parejas? (Asume que una pareja está conformada por un chico y una chica).
• (b) Como ninguna chica ha quedado contenta con el desempeño en el baile de su pareja, de cara a la segunda canción, ¿de cuántas maneras pueden organizarse para bailar por parejas de forma que no repitan con la anterior?

Solución: para el apartado (a), consideremos, sin pérdida de generalidad, que las chicas escogen su pareja. La primera de ellas dispone, para su elección, de seis opciones, tantas como chicos han acudido a la fiesta. La segunda chica, una vez haya escogido la primera, puede seleccionar su pareja de entre los cinco chicos restantes, y así sucesivamente. Por tanto, utilizando la regla del producto, se pueden organizar de

$$ 6\cdot5\cdot4\cdot3\cdot2\cdot1 = 6! = 720 $$

formas posibles para bailar por parejas la primera canción.

Alternativamente, y pensando ya más bien en el próximo apartado, imaginemos que la situación a la hora de emparejarse se produce como sigue: situemos en una fila a los chicos y, en frente de ellos, en otra fila parelela a las chicas. Ellas poseen en sus manos un papel con un número del $1$ al $6$, al igual que ellos. Supongamos que los números de los chicos están ordenados de menor a mayor, situación que, abreviadamente, denotaremos por $123456$. Después, dejamos que las chicas intercambien sus posiciones entre ellas como deseen y saquen a bailar al chico que al final tengan en frente. Así, las chicas podrían ordenarse, en función de los números que llevan entre manos, como $654321$ y se formarían las parejas de baile $(1,6)$, $(2,5)$, $(3,4)$, $(4,3)$, $(5,2)$ y $(6,1)$, que podemos denotar de forma más abreviada como $123456\rightarrow 654321$. La pregunta que surge ahora es, ¿de cuántas maneras pueden ordenarse las seis chicas? Efectivamente, como el orden es importante y no es posible repetir elemento alguno (una chica no puede bailar a la vez con dos chicos), el total de formas coincide con la cantidad de permutaciones de seis elementos, esto es, $P_6 = 6! = 720$ maneras posibles.

En cuanto al apartado (b), comencemos reduciendo un poco la magnitud del problema, para así visualizar cómo abordarlo. Consideremos únicamente tres chicos y tres chicas, y supongamos, por ejemplo, que para la primera canción las parejas se conformaron fueron $123\rightarrow 123$. Como en la segunda canción ninguna de ellas quiere repetir con la pareja anterior, las dos únicas opciones disponibles serían $123\rightarrow 231$ y $123\rightarrow 312$, esto es, los dos desarreglos.

Por el ejercicio anterior, y ya volviendo al problema que contempla seis chicos y seis chicas, sabemos que

$$ D_6 = 6!\left(\dfrac{1}{2} - \dfrac{1}{6} + \dfrac{1}{24} - \dfrac{1}{120} + \dfrac{1}{720}\right) = 265 $$

son las maneras en que pueden organizarse, para bailar por parejas los seis chicos y las seis chicas, de forma que no repitan con la anterior.

Problema 15

¿Cuántos números naturales menores que $10000$ cumplen que la suma de sus cifras es $25$?

Solución: los números $n$ que nos interesan satisfacen que $0\leq n\leq 9999$, esto es, pueden tener hasta cuatro cifras. Como la suma de estas debe ascender a $25$, planteamos la ecuación

$$ x_1+x_2+x_3+x_4=25, $$

donde $0\leq x_i\leq 9$, con $1\leq i\leq 4$ y representando cada $x_i$ una de las cifras de los números buscados.

En ejercicios anteriores analizamos cómo encontrar todas las soluciones enteras no negativas de una ecuación como la planteada, e incluso vimos cuál era la forma de proceder cuando algunas de las variables quedaban afectadas por restricciones de mayor o igual. La forma de resolver este tipo de problemas, cuando surgen restricciones de menor o igual afectando a las variables, será la siguiente: utilizaremos el Principio de complementación, de forma que calcularemos el número de soluciones enteras no negativas de la ecuación propuesta y, después, haciendo uso del Principio de inclusión-exclusión, descontaremos aquellas que no satisfagan las restricciones impuestas.

Así pues, empecemos planteando la ecuación

$$ x_1+x_2+x_3+x_4=25, $$

con $x_i\geq 0$ para todo $1\leq i\leq 4$. Consideremos ahora las cuatro variables como cuatro urnas indistinguibles y el valor que aparece en el miembro derecho de la ecuación, $25$, como las $25$ bolas idénticas que vamos a introducir en las urnas. Utilizando la estrategia de barras y estrellas, necesitamos tres barras para representar sobre la recta real las cuatro urnas y buscamos ubicar luego $25$ estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que el valor de la suma de cuatro variables puede ascender a $25$, equivale a la cantidad de permutaciones con repetición de $28$ elementos, donde uno de ellos se repite tres veces, mientras que el otro lo hace en $25$ ocasiones. Así, hay

$$ PR_{28}^{3,25} = CR_{4,25} = \dbinom{28}{25} = \dfrac{28\cdot27\cdot26}{3!} = 3276 $$

soluciones enteras no negativas para la ecuación que acabamos de plantear. Entre ellas, será válida, por ejemplo, una solución como $x_1=25$ y $x_2=x_3=x_4=0$, que en el contexto que plantea el enunciado del presente ejercicio es absurda, pues recordemos habíamos dotado a cada una de las variables el significado de ser cifras y, por tanto, sus valores han de estar comprendidos entre cero y nueve. Veamos pues, a continuación, como descontar este tipo de soluciones incorrectas.

Definamos, acto seguido, los conjuntos $A_i=\{x_i\geq 10\}$, por lo que estamos interesados en hallar el valor de $card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_4})$. Por el Principio de complementación,

$$ card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_4}) = card(E) - card(A_1\cup A_2\cup A_3\cup A_4), $$

donde por $E$ representamos al conjunto total, que en este contexto se refiere al total de soluciones enteras no negativas de la ecuación planteada y cuyo cardinal hemos obtenido en párrafos anteriores, $PR_{28}^{3,25} = 3276$. Aplicando ahora el principio de inclusión-exclusión,

$$ \begin{aligned} card\left(\bigcup_{i=1}^{4}{A_i}\right) &= \sum_{i=1}^{4}{card(A_i)} - \sum_{1\leq i < j\leq 4}{card( A_i\cap A_j )} + \cdots\\ &+ (-1)^{n+1} card\left(\bigcap_{i=1}^{4}{A_i}\right). \end{aligned} $$

Estudiemos ahora el conjunto $A_1 = \{x_1\geq 10\}$ y averigüemos $card(A_1)$. La situación requiere calcular el número de soluciones enteras no negativas para la ecuación $x_1+x_2+x_3+x_4=25$, con $x_1\geq 10$, $x_i\geq 0$ para $2\leq i\leq 4$. Pensando en términos de urnas y bolas, hemos de almacenar diez bolas en la primera urna y pasar a encontrar entonces el número de soluciones enteras no negativas de la ecuación $x_1+x_2+x_3+x_4=15$, ahora con $x_i\geq 0$, para $1\leq i\leq 4$. Aplicando, de manera análoga a como lo hicimos arriba, la técnica de barras y estrellas, sabemos que dicho número equivale al total de permutaciones con repetición de $18$ elementos, donde uno de ellos se repite tres veces, mientras que el otro lo hace en $15$ ocasiones, esto es,

$$ PR_{18}^{3,15} = CR_{4,15} = \dbinom{18}{15} = \dfrac{18\cdot17\cdot16}{3!} = 816. $$

Por simetría, $card(A_1)=card(A_2)=card(A_3)=card(A_4)=816$, de manera que

$$ \sum_{i=1}^{4}{card(A_i)} = 4\cdot816 = 3264. $$

Ahora, hallemos $card(A_1\cap A_2)$, donde $A_1\cap A_2 = \{x_1\geq 10, x_2\geq 10\}$. La situación requiere calcular el número de soluciones enteras no negativas para la ecuación $x_1+x_2+x_3+x_4=25$, con $x_1\geq 10$, $x_2\geq 10$ y $x_i\geq 0$ para $3\leq i\leq 4$. Razonando en términos de urnas y bolas, hemos de almacenar diez bolas en la primera urna, otras tantas en la segunda urna y pasar a buscar entonces el número de soluciones enteras no negativas de la ecuación $x_1+x_2+x_3+x_4=5$, ahora con $x_i\geq 0$, para $1\leq i\leq 4$. Utilizando, como antes, la técnica de barras y estrellas, sabemos que el mencionado número equivale al total de permutaciones con repetición de ocho elementos, donde uno de ellos se repite tres veces, mientras que el otro lo hace en cinco ocasiones, es decir,

$$ PR_{8}^{3,5} = CR_{4,5} = \dbinom{8}{5} = \dfrac{8\cdot7\cdot6}{3!} = 56. $$

Por simetría, el resto de cardinales de los conjuntos $A_{i} \cap A_{j}$, con $1\leq i < j \leq 4$ ascenderán al mismo valor. Como el orden en el que seleccionemos los conjuntos implicados no tiene relevancia y no existe posibilidad de repetir elemento alguno, en total su número será igual a la cantidad de combinaciones de cuatro elementos tomados de dos en dos, $C_{4,2}$, luego

$$ \sum_{1 \leq i < j \leq 4}{card(A_{i} \cap A_{j})} = C_{4,2} \cdot PR_{8}^{3,5} = \dbinom{4}{2}\cdot 56 = 336. $$

Acto seguido, el cardinal de los conjuntos $A_i\cap A_j\cap A_k$, con $1\leq i<j<k\leq 4$ y el del conjunto $A_1\cap A_2\cap A_3\cap A_4$ será cero, pues si tres o más variables poseen un valor mayor o igual que diez, es imposible satisfacer la ecuación $x_1+x_2+x_3+x_4=25$ en los enteros no negativos. Por tanto, recapitulando,

$$ card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3} \cap \overline{A_4}) = 3276 - (3264 - 336) = 346 $$

son los números naturales menores que $10000$ que cumplen que la suma de sus cifras es $25$.

Problema 16

En el lanzamiento simultáneo de tres dados distintos, ¿de cuántas maneras la suma de las puntuaciones puede ascender a diez?

Solución: si asumimos que trabajamos con tres dados estándar y representamos por $x_i$ la puntuación obtenida en el lanzamiento del $i$-ésimo dado, con $1\leq i\leq 3$, buscamos encontrar el número de soluciones enteras de la ecuación $x_1+x_2+x_3 = 10$, donde $1\leq x_i\leq 6$, para $1\leq i\leq 3$.

Seguiremos, a continuación, el mismo esquema que figura en el ejercicio anterior, esto es, utilizaremos el Principio de complementación, de forma que calcularemos el número de soluciones enteras no negativas (que satisfagan las restricciones de mayor o igual para las variables involucradas) de la ecuación propuesta y, después, haciendo uso del Principio de inclusión-exclusión, descontaremos aquellas que no satisfagan las restricciones impuestas.

Así pues, empecemos planteando la ecuación $x_1+x_2+x_3=10$, con $x_i\geq 1$ para todo $1\leq i\leq 3$. Pensando en términos de urnas y bolas, hemos de almacenar una bola en cada urna y pasar a encontrar entonces el número de soluciones enteras no negativas de la ecuación $x_1+x_2+x_3=7$, ahora con $x_i\geq 0$, para $1\leq i\leq 3$. Aplicando la técnica de barras y estrellas, como en ejercicios previos, sabemos que dicho número equivale al total de permutaciones con repetición de nueve elementos, donde uno de ellos se repite dos veces, mientras que el otro lo hace en siete ocasiones, esto es,

$$ PR_{9}^{2,7} = CR_{3,7} = \dbinom{9}{7} = \dfrac{9\cdot8}{2!} = 36. $$

Definamos, acto seguido, los conjuntos $A_i = \{x_i\geq 7\}$, para $1\leq i\leq 3$, por lo que estamos interesados en hallar el valor de $card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3})$. Por el Principio de complementación,

$$ card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}) = card(E) - card(A_1\cup A_2\cup A_3), $$

donde por $E$ representamos al conjunto total, que en este contexto se refiere al total de soluciones enteras no negativas de la ecuación planteada y cuyo cardinal hemos obtenido en párrafos anteriores, $PR_{9}^{2,7} = 36$. Aplicando ahora el principio de inclusión-exclusión,

$$ card\left( \bigcup_{i = 1}^{3}{A_{i}} \right) = \sum_{i = 1}^{3}{card(A_{i})} - \sum_{1 \leq i < j \leq 3}{card(A_{i} \cap A_{j})} + card\left( \bigcap_{i = 1}^{3}{A_{i}} \right). $$

Estudiemos ahora el conjunto $A_1 = \{x_1\geq 7\}$ y averigüemos $card(A_1)$. La situación requiere calcular el número de soluciones enteras no negativas para la ecuación $x_1+x_2+x_3=10$, con $x_1\geq 7$, $x_i\geq 1$ para $2\leq i\leq 3$. Pensando en términos de urnas y bolas, hemos de almacenar siete bolas en la primera urna, una en la segunda, una en la tercera y pasar a encontrar entonces el número de soluciones enteras no negativas de la ecuación $x_1+x_2+x_3=1$, ahora con $x_i\geq 0$, para $1\leq i\leq 3$. Aplicando, de manera análoga a como lo hicimos arriba, la técnica de barras y estrellas, sabemos que dicho número equivale al total de permutaciones con repetición de tres elementos, donde uno de ellos se repite dos veces, mientras que el otro lo hace en una ocasión, esto es,

$$ PR_{3}^{1,2} = CR_{3,1} = \dbinom{3}{1} = 3. $$

Por simetría, $card(A_1)=card(A_2)=card(A_3)=3$, de manera que

$$ \sum_{i=1}^{3}{card(A_i)} = 9. $$

Por lo que respecta al resto de casos, cuando intersecamos dos o más conjuntos las restricciones imponen una suma mayor o igual que $14$, por lo que es imposible que se satisfaga en enteros no negativos la ecuación $x_1+x_2+x_3=10$, esto es, los cardinales asociados a las correspondientes intersecciones serán nulos.

Por tanto, recapitulando,

$$ card(\overline{A_1} \cap \overline{A_2} \cap \overline{A_3}) = 36-9 = 27 $$

son las maneras en las que, en el lanzamiento simultáneo de tres dados distintos, la suma de las puntuaciones asciende a diez.

Problema 17

Trazamos en un plano $n$ rectas secantes dos a dos, pero tres a tres no concurrentes, ¿en cuántas regiones queda dividido el plano?

Solución: claramente observamos, en la siguiente imagen, que dos rectas secantes dividen el plano en cuatro regiones. Al añadir una nueva recta, de manera que las tres no sean concurrentes en un punto, necesariamente aparecerán dos nuevos puntos de intersección con las rectas originales (puesto que la incorporada no puede ser paralela a las existentes, al existir la restricción de que las rectas sean secantes dos a dos), hecho que implica que la recta subdivide en dos tres de las cuatro regiones en las que se encontraba dividido el plano, produciendo entonces en total siete regiones ($4 + 3 = 7$).

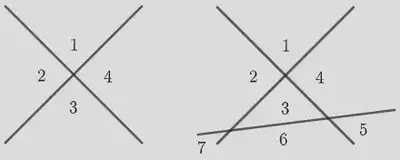
Una cuarta recta, que fuese secante dos a dos con las tres anteriores, daría lugar a tres nuevos puntos de intersección, situación que provocaría que cuatro de las anteriores regiones quedasen, cada una de ellas, subdividas en dos nuevas regiones. En total, contaríamos pues con once regiones ($7 + 4 = 11$).

En general, denotemos por $R_n$ al número de regiones en que el plano queda dividido por $n$ rectas que son secantes dos a dos, pero tres a tres no concurrentes. Al incorporar una nueva recta, que será secante dos a dos con todas las anteriores, esta dará lugar a $n$ nuevos puntos de intersección (ya que no será concurrente tres a tres con ninguno de los pares presentes), hecho que provoca que, de las $R_n$ regiones que se contaban antes de introducir la nueva recta, $n+1$ queden, cada una de ellas, subdividas en dos regiones. Así, es cierto que, para cada número natural $n$,

$$ R_{n+1} = R_n + (n+1), $$

dando lugar a una ecuación en diferencias lineal completa de orden uno. Su ecuación homogénea asociada es $R_{n+1} - R_n = 0$, con ecuación característica correspondiente $\lambda - 1 = 0$, esto es, $\lambda = 1$. Así, la solución para dicha ecuación homogénea es $R_h = c_1$, con $c_1\in\mathbb{R}$.

Ahora, como el término independiente, $n+1$, es un polinomio de grado uno en $n$ y $\lambda = 1$ es una raíz simple de la ecuación característica, proponemos como solución particular $n^1(an+b) = an^2+bn$ y sustituyendo en la ecuación en diferencias inicial, queda

$$ a(n+1)^2 + b(n+1) - an^2 - bn = n+1. $$

Operando, llegamos a que $2an + (a+b) = n+1$ e igualando coeficientes $a = b = 1 / 2$, por lo que la solución particular a la ecuación en diferencias planteada es, para cada número natural $n$, $R_p = (n^2+n) / 2$.

Por consiguiente, la solución general a la ecuación en diferencias propuestas, que es la suma de la solución para la ecuación homogénea y la solución particular, es

$$ R_n = c_1 + \dfrac{n^2+n}{2}, $$

con $c_1\in\mathbb{R}$. Dado que para $n = 2$ hemos establecido, al principio del ejercicio, que $R_2 = 4$, sustituyendo podemos averiguar el valor de $c_1$. Así,

$$ 4 = c_1 + \dfrac{2^2+2}{2}, $$

esto es, $c_1 = 1$ y concluimos que, para cada número natural $n$,

$$ R_n = \dfrac{n^2+n+2}{2} $$

es el número de regiones en que queda dividido un plano cuando trazamos $n$ rectas secantes dos a dos, pero tres a tres no concurrentes.

Alternativamente, por tanteo de unos cuantos casos particulares para los primeros valores de $n$, obtenemos la siguiente tabla

$n$	$1$	$2$	$3$	$4$	$5$	$6$
$R_n$	$2$	$4$	$7$	$11$	$16$	$22$
$\Delta R_n$	$2$	$3$	$4$	$5$	$6$	$7$
$\Delta^2 R_n$	$1$	$1$	$1$	$1$	$1$	$1$

Por consiguiente, la sucesión $(R_n)$ es una progresión aritmética de orden dos, luego, por los resultados teóricos asociados a este tipo de sucesiones,

$$ \begin{aligned} R_n &= \dbinom{n-1}{0}R_1 + \dbinom{n-1}{1}\Delta R_1 + \dbinom{n-1}{2}\Delta^2 R_1\\ &= 1\cdot2 + (n-1)\cdot2 + \dfrac{(n-1)(n-2)}{2}\cdot1\\ &= \dfrac{4 + 4(n-1) + (n-1)(n-2)}{2}\\ &= \dfrac{n^2 +n+2}{2}, \end{aligned} $$

arribando al mismo resultado que antes.

Problema 18

Calcula el número de soluciones enteras no negativas de la inecuación

$$ x+y+z+t \leq 2001. $$

Solución: a diferencia de ejercicios anteriores, en el presente encontramos una inecuación en lugar de una ecuación. Razonando en términos de urnas indistinguibles y bolas idénticas, esta situación se traduce en que, para ciertos repartos, algunas de las $2001$ bolas pueden quedar fuera de las cuatro urnas que emplearíamos para representar las variables $x$, $y$, $z$ y $t$. Así pues, procederemos generando una urna adicional, para una variable $u$, que será aquella donde depositemos el exceso de bolas del reparto. Por tanto, la inecuación planteada quedaría ahora como la ecuación

$$ x+y+z+t+u=2001, $$

de la cual deseamos encontrar el número de soluciones enteras no negativas.

Ahora ya estamos en condiciones de volver a utilizar las estrategias vistas en ejercicios previos. Aplicando la técnica de barras y estrellas, necesitamos cuatro barras para representar sobre la recta real las cinco urnas y buscamos ubicar luego $2001$ estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que el valor de la suma de cinco variables puede ascender a $2001$, equivale a la cantidad de permutaciones con repetición de $2005$ elementos, donde uno de ellos se repite cuatro veces, mientras que el otro lo hace en $2001$ ocasiones. Así, hay

$$ \begin{aligned} PR_{2005}^{4, 2001} &= CR_{5, 2001} = \dbinom{2005}{2001}= \dfrac{2005\cdot2004\cdot2003\cdot2002}{4!}\\ &= 671345179505 \end{aligned} $$

soluciones enteras no negativas para la ecuación propuesta y, por tanto, asimismo para la inecuación planteada en el enunciado del ejercicio.

Problema 19

• (a) Calcula el número de soluciones enteras no negativas de

$$ x_1+x_2+x_3+x_4+x_5+x_6=10. $$

• (b) ¿Cuántas soluciones enteras no negativas posee la inecuación

$$ x_1+x_2+x_3+x_4+x_5+x_6 < 10 ? $$

Solución: para el apartado (a), razonaremos, como viene siendo ya habitual, en términos de urnas indistinguibles y bolas idénticas. Consideraremos que tenemos en nuestro haber seis de dichas urnas, en las que deseamos colocar diez de las mencionadas bolas. Aplicando la técnica de barras y estrellas necesitamos cinco barras para representar sobre la recta real las seis urnas y buscamos ubicar luego diez estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que el valor de la suma de seis variables puede ascender a diez, equivale a la cantidad de permutaciones con repetición de $15$ elementos, donde uno de ellos se repite cinco veces, mientras que el otro lo hace en diez ocasiones. Así, hay

$$ PR_{15}^{5,10} = CR_{6,10} = \dbinom{15}{10} = \dfrac{15\cdot14\cdot13\cdot12\cdot11}{5!} = 3003 $$

soluciones enteras no negativas para la ecuación propuesta.

En cuanto al apartado (b), nos encontramos en una situación parecida a la del ejercicio anterior, aunque observamos una desigualdad estricta. En primer lugar, cambiaremos adecuadamente el signo $<$ por $\leq$ y luego procederemos como en aquel problema. Así, como estamos interesados en soluciones enteras no negativas, es cierto que

$$ x_1+x_2+x_3+x_4+x_5+x_6 < 10 \Leftrightarrow x_1+x_2+x_3+x_4+x_5+x_6\leq 9. $$

A continuación, introducimos una urna adicional, en la forma de una nueva variable, $x_7$, para así transformar la inecuación en una ecuación. Por tanto, el problema se reduce a averiguar el número de soluciones enteras no negativas de la ecuación

$$ x_1+x_2+x_3+x_4+x_5+x_6+x_7=9. $$

Aplicando la técnica de barras y estrellas necesitamos seis barras para representar sobre la recta real las siete urnas y buscamos ubicar luego nueve estrellas en los huecos que dicha configuración produce. Por consiguiente, el número de formas en que el valor de la suma de siete variables puede ascender a nueve, equivale a la cantidad de permutaciones con repetición de $15$ elementos, donde uno de ellos se repite seis veces, mientras que el otro lo hace en nueve ocasiones. Así, hay

$$ PR_{15}^{6,9} = CR_{7,9} = \dbinom{15}{9} = \dfrac{15\cdot14\cdot13\cdot12\cdot11\cdot10}{6!} = 5005 $$

soluciones enteras no negativas para la ecuación propuesta y, por tanto, asimismo para la inecuación planteada en el segundo apartado del ejercicio.

Problema 20

Demuestra que, para cada número natural $n$,

$$ \dbinom{-1 / 2}{n} = \dbinom{2n}{n}\left(-\dfrac{1}{4}\right)^n. $$

Solución: utilizando la definición,

$$ \begin{aligned} \dbinom{-1 / 2}{n} &= \dfrac{\left(-\dfrac{1}{2}\right)\left(-\dfrac{1}{2}-1\right)\left(-\dfrac{1}{2}-2\right)\cdots\left(-\dfrac{1}{2} - (n-1)\right)}{n!}\\ &= \dfrac{\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)\left(-\dfrac{5}{2}\right)\cdots\left(\dfrac{1-2n}{2}\right)}{n!}. \end{aligned} $$

En el numerador encontramos $n$ factores, por lo que podremos extraer esa misma cantidad de signos negativos, quedando entonces $(-1)^n$ (atención a cómo quedaría el último factor tras esta acción). Además, hay $n$ doses en los denominadores de las fracciones que aparecen en el numerador, quedando su producto entonces $2^n$, valor que podemos trasladar al denominador de la expresión. Por consiguiente,

$$ \dbinom{-1 / 2}{n} = (-1)^n \cdot\dfrac{1\cdot3\cdot5\cdots (2n-1)}{2^n n!}. $$

Ahora, multipliquemos y dividamos por el producto de números pares $2\cdot4\cdot6\cdots 2n$ (llegamos a $2n$ y no hasta $2n-2$ por la expresión a la que buscamos arribar), provocando así que en el numerador aparezca el factorial de $2n$,

$$ \begin{aligned} \dbinom{-1 / 2}{n} &= (-1)^n\dfrac{1\cdot2\cdot3\cdot4\cdot5\cdots (2n-1)\cdot 2n}{(2\cdot4\cdot6\cdots 2n) 2^n n!}\\ &= (-1)^n\dfrac{(2n)!}{(2\cdot4\cdot6\cdots 2n) 2^n n!}. \end{aligned} $$

Además, sacando un dos de cada factor, y teniendo en cuenta que hay $n$ de ellos, es cierto que,

$$ 2\cdot4\cdot6\cdots 2n = 2^n(1\cdot2\cdot3\cdots n) = 2^n n!, $$

y sustituyendo el resultado alcanzado en la expresión anterior,

$$ \dbinom{-1 / 2}{n} = (-1)^n\dfrac{(2n)!}{(2^n n!) (2^n n!)}. $$

Como $2^n\cdot 2^n = 2^{2n} = 4^n$,

$$ \dbinom{-1 / 2}{n} = (-1)^n\dfrac{(2n)!}{4^n n! n!} = \dfrac{(-1)^n}{4^n}\dbinom{2n}{n} = \dbinom{2n}{n}\left(-\dfrac{1}{4}\right)^n , $$

tal y como queríamos demostrar.

Problema 21

¿Cuántas rutas existen, desde la esquina inferior izquierda de una cuadrícula $n\times n$ a la esquina superior derecha, si los viajes se restringen solo a pasos de longitud unitaria a la derecha o hacia arriba?

Solución: antes de abordar el problema en su versión general, tal y como reza el enunciado, estudiemos un caso concreto, como el que se muestra en la siguiente figura. En ella, hemos tomado $n=5$ y sobre la cuadrícula aparecen delineadas dos de las posibles rutas (una en verde y otra en rojo) que parten del origen de coordenadas $(0,0)$ y llegan hasta el punto $(5,5)$. Esto es, ambas parten desde la esquina inferior izquierda de la mencionada cuadrícula y arriban a su esquina superior derecha.

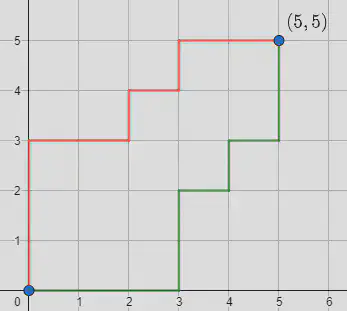
Si denotamos por $D$ a los pasos de longitud unitaria que se recorren hacia la derecha y por $A$ a los correspondientes que se efectúan hacia arriba, rápidamente apreciamos que, en cada una de las rutas que podamos imaginar, habrá cinco $D$ y otras cinco $A$. Es decir, toda ruta es una reordenación de la cadena $DDDDDAAAAA$. El número de tales cadenas que podemos escribir asciende al total de permutaciones con repetición de diez elementos, donde uno de ellos se repite cinco veces, mientras que el otro lo hace en el mismo número de ocasiones. Así, hay

$$ PR_{10}^{5,5} = \dfrac{10!}{5!5!} = \dfrac{10\cdot9\cdot8\cdot7\cdot6}{5!} = 252 $$

rutas posibles cuando $n=5$.

Alternativamente, podemos enfocar el problema como sigue: para llegar desde una esquina a la otra es necesario que efectuemos un total de diez de pasos, de los cuales cinco habrán de ser hacia la derecha (el mismo razonamiento es válido si consideramos dar los pasos hacia arriba). Como el orden en el que los demos no es importante, el número de maneras de dar cinco pasos a la derecha de un total de diez pasos equivale al total de combinaciones de diez elementos tomados de cinco es cinco, es decir,

$$ C_{10,5} = \dbinom{10}{5} = \dfrac{10\cdot9\cdot8\cdot7\cdot6}{5!} = 252. $$

Si ahora consideramos una cuadrícula rectangular, de manera que la esquina superior derecha de la misma la situamos en el punto $(5,7)$, razonaríamos de manera análoga a como hicimos en el párrafo anterior. ¿Cuántos pasos hemos de efectuar para llegar desde el origen de coordenadas hasta el punto $(5,7)$? En las condiciones que impone el enunciado del ejercicio, serían $5+7=12$ los pasos requeridos. El número de rutas, entonces, ascendería al total de combinaciones de doce elementos tomados de cinco en cinco, $C_{12,5}$ (o bien $C_{12,7}$ si hacemos el razonamiento fijándonos en los pasos que deben darse hacia arriba), esto es,

$$ C_{12,5} = C_{12,7} = \dbinom{12}{5} = \dfrac{12\cdot11\cdot10\cdot9\cdot8}{5!} = 792 $$

son las rutas posibles en este caso.

En general, dada una cuadrícula $m\times n$ el número de rutas que existen, desde su esquina inferior izquierda hasta su esquina superior derecha, si los viajes se restringen a pasos de longitud unitaria a la derecha o hacia arriba asciende a

$$ C_{m+n,n} = \dbinom{m+n}{n}\qquad\text{o}\qquad C_{m+n,m}=\dbinom{m+n}{m}. $$

En nuestro caso concreto, como $m=n$, dicha cifra será

$$ C_{2n,n} = \dbinom{2n}{n}. $$

Imaginemos, a continuación, que nos indican que estamos situados en el punto $(1,2)$. ¿Cuántas rutas distintas existen desde dicho punto a la esquina superior derecha de la cuadrícula, $(n,n)$? Esta cuestión la resolveríamos aplicando una traslación, puesto que el número de rutas entre los puntos $(1,2)$ y $(n,n)$ equivale al total de rutas entre $(0,0)$ y $(n-1,n-2)$ (simplemente hemos efectuado una traslación de vector $(1,2)$, es decir, sustraemos el mencionado vector a ambos puntos para obtener los finalmente mostrados). Dicha cifra, aplicando lo visto en párrafos anteriores, será

$$ \dbinom{n-1+n-2}{n-1} = \dbinom{2n-3}{n-1} = C_{2n-3,n-1} $$

o bien $C_{2n-3,n-2}$.

Consideremos ahora que la longitud de una ruta equivale al número de pasos realizados. Así, podríamos preguntamos, ¿cuántas rutas de longitud seis existen? Una ruta de longitud seis, en las condiciones que impone en el enunciado de este ejercicio, puede llevarnos a cualquiera de los puntos que se indican en la siguiente figura, por lo que la tarea se reduce entonces a contar el número de rutas existente desde el origen de coordenadas a cada uno de ellos.

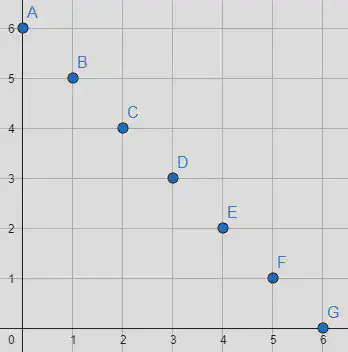
Así, de $(0,0)$ a $(0,6)$ hay un total de $C_{6,0}$ rutas; de $(0,0)$ a $(1,5)$ encontramos $C_{6,1}$ rutas; de $(0,0)$ a $(2,4)$ hallamos $C_{6,2}$ rutas; y así sucesivamente. En total son

$$ \dbinom{6}{0} + \dbinom{6}{1} + \dbinom{6}{2} + \dbinom{6}{3} + \dbinom{6}{4} + \dbinom{6}{5} + \dbinom{6}{6} = 2^6 = 64, $$

ya que,

$$ \dbinom{n}{0} + \dbinom{n}{1} + \dbinom{n}{2} + \cdots + \dbinom{n}{n} = \sum_{k=0}^{n}{\dbinom{n}{k}} = (1+1)^n = 2^n. $$

Por tanto, si ahora nos preguntasen por el total de rutas de longitud diez, directamente podríamos decir que son $2^{10} = 1024$.

Este clásico problema, conocido como el de las rutas equiprobables, nos permite dar respuesta a preguntas como: ¿de cuántas maneras podemos obtener cinco caras y cinco cruces al lanzar una moneda diez veces? En ejercicios anteriores, utilizando técnicas de combinatoria, hallamos que dicha cantidad equivalía a $PR_{10}^{5,5}$ o bien $C_{10,5}$. Un enfoque alternativo sería por conteo de rutas desde el origen de coordenadas hasta el punto de interés, $(5,5)$ en esta ocasión. Por otro lado, el total de rutas de longitud seis es, en otros términos, la cantidad de secuencias que podemos obtener al lanzar una moneda seis veces, que, por combinatoria, sabemos asciende a $VR_{2,6} = 2^6 = 64$. Así, los ejercicios de rutas fácilmente se extrapolan a otros contextos (sobre todo de monedas) y podemos resolver con ellas interrogantes del estilo: dado que he obtenido una cada y dos cruces, ¿de cuántas formas posibles puedo llegar a conseguir diez caras y diez cruces? La respuesta, como vimos en párrafos anteriores, la encontraríamos rápidamente tras aplicar una traslación de vector $(1,2)$ y contar después del número de rutas entre el origen de coordenadas y el punto $(9,8)$.

Problema 22

Sea el plano $E$ cuadriculado por las rectas $x=m$ e $y=n$, con $m$ y $n$ números enteros. El punto $P(m,n)$ es un nudo de la cuadrícula. Una sucesión de nudos se llama trayectoria. Se consideran las trayectorias ascendentes $T_a$ en las que se pasa de un nudo al siguiente por la traslación $u$ o por la traslación $v$, donde $(O,u,v)$ es un sistema ortogonal. La longitud de una trayectoria es el número de traslaciones $u$ o $v$ que tiene.

• (a) Determina el número $T_{a}(O,P)$ que va desde el origen $O$ hasta el punto $P(m,n)$ ($m\geq0$, $n\geq0$) y el número de trayectorias $T^{\prime}_{a}( P^{\prime}, P )$ que van del punto $P^{\prime} ( m^{\prime}, n^{\prime} )$ al punto $P(m,n)$ con $m^{\prime}\leq m$ y $n^{\prime}\leq n$.
• (b) Calcula el número de trayectorias de longitud $h$, $T_a$, que parten del origen.
• (c) Sea $P(m,n)$, con $m>n$. Calcula el número $T_{a_1}(O,P)$ de trayectorias que van de $O$ a $P$ por debajo de la diagonal $y=x$.
• (d) Sea $P(n,n)$. Halla el número de trayectorias $T_{a_2}(O,P)$ que van de $O$ a $P$ por encima o por debajo de la diagonal principal sin tocarla nada más que en los puntos $O$ y $P$.
• (e) Se lanza una moneda $2n$ veces, ¿cuál es la probabilidad de obtener $n$ caras y $n$ cruces? Se supone que la igualdad no se alcanza antes del último lanzamiento.

Solución: el presente problema, en planteamiento, es similar (en parte) al que figura en el problema anterior, de manera que haremos uso aquí de algunos de los resultados alcanzados allí. Así, la situación que se plantea queda ilustrada en el siguiente diagrama.

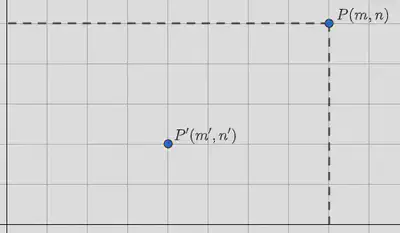
En el apartado (a) nos piden obtener el número de trayectorias (que en el ejercicio anterior designábamos por rutas) desde el origen de coordenadas hasta el punto $P(m,n)$. Sabemos que dicha cifra se corresponde con la elección de $m$ posibilidades tomadas de un total de $m+n$, esto es,

$$ C_{m+n,m} = \dbinom{m+n}{m}, $$

cantidad que es equivalente, asimismo, a $C_{m+n,n}$ o a $PR_{m+n}^{m,n}$.

A continuación, para la segunda parte de este apartado, hemos de encontrar el total de rutas existentes entre los puntos $P^{\prime} ( m^{\prime}, n^{\prime} )$ y $P(m,n)$. Dicha cifra es equivalente, por traslación, al número de rutas entre el origen de coordenadas y el punto $(m,n) - ( m^{\prime}, n^{\prime} ) = ( m - m^{\prime}, n - n^{\prime} )$. Por tanto, hay

$$ C_{m+n-m^{\prime}-n^{\prime}, m-m^{\prime}} = \dbinom{m+n-m^{\prime}-n^{\prime}}{m-m^{\prime}} $$

rutas existentes entre los puntos $P^{\prime} ( m^{\prime}, n^{\prime} )$ y $P(m,n)$.

Para el apartado (b), por el razonamiento que se encuentra en el ejercicio citado, concluimos que el número de trayectorias de longitud $h$ es

$$ \dbinom{h}{0} + \dbinom{h}{1} + \dbinom{h}{2} + \cdots + \dbinom{h}{h} = 2^h. $$

Acto seguido, para el apartado (c), nos apoyaremos en el diagrama que aparece en la siguiente figura, donde hemos añadido al anterior la recta diagonal de ecuación $y=x$.

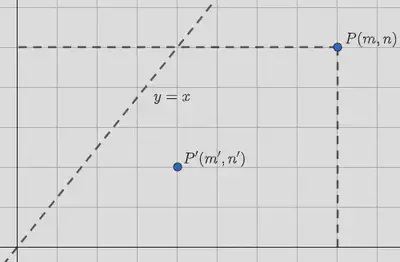
Buscamos todas las rutas existentes entre el origen de coordenadas y el punto $P(m,n)$ que se sitúen por debajo de la mencionada diagonal, esto es, que no posean intersección con ella. Obligatoriamente, todas ellas empezarán desde el punto $(1,0)$, ya que de hacerlo desde $(0,1)$, parte de la ruta se situaría por encima de la diagonal $y=x$.

Así pues, hallemos el total de rutas existentes entre el punto $(1,0)$ y el punto $P(m,n)$ que, por traslación, sabemos es equivalente a la cantidad de rutas entre el origen de coordenadas y el punto $(m,n) - (1,0) = (m-1,n)$ y esta última cifra asciende a

$$ C_{m+n-1,n} = \dbinom{m+n-1}{n}. $$

No obstante, entre ellas habrá algunas que se caractericen por intersecar la diagonal $y=x$, que procedemos a sustraer utilizando el Principio de reflexión de André. Aplicado a este caso particular, dicho principio afirma que el número de trayectorias que van desde el punto $(1,0)$ hasta el punto $P(m,n)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,1)$ (simétrico de $(1,0)$ respecto de la recta $y=x$) hasta el punto $P(m,n)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (0,1) = (m,n-1)$, esto es,

$$ C_{m+n-1,m} = \dbinom{m+n-1}{m}. $$

Por consiguiente, el número de trayectorias desde el origen de coordenadas hasta el punto $P(m,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son

$$ \dbinom{m+n-1}{n} - \dbinom{m+n-1}{m}. $$

Siendo estrictos, en realidad el primer punto de partida es $(2,0)$ y no $(1,0)$, puesto que si de este último efectuamos un ‘‘paso hacia arriba’’ se produciría una intersección con la recta diagonal $y=x$. No obstante, el Principio de reflexión de André nos permite empezar, sin problema alguno, desde $(1,0)$, ya que descontará las rutas que no satisfagan la condición impuesta en el enunciado para este apartado. No obstante, si optamos por empezar desde $(2,0)$, el procedimiento a seguir es análogo al mostrado en párrafos anteriores. El total de rutas de rutas desde el punto $(2,0)$ al punto $P(m,n)$, por traslación, equivale a la cantidad de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (2,0) = (m-2,n)$, esto es,

$$ C_{m+n-2,n} = \dbinom{m+n-2}{n}. $$

Ahora, por el Principio de reflexión de André, el número de trayectorias que van desde el punto $(2,0)$ hasta el punto $P(m,n)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,2)$ (simétrico de $(2,0)$ respecto de la recta $y=x$) hasta el punto $P(m,n)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (0,2) = (m,n-2)$, esto es,

$$ C_{m+n-2,m} = \dbinom{m+n-2}{m}. $$

Por tanto, el número de trayectorias desde el origen de coordenadas hasta el punto $P(m,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son

$$ \dbinom{m+n-2}{n} - \dbinom{m+n-2}{m}, $$

y esta diferencia coincide con la calculada anteriormente.

En el apartado (d), la situación se ilustra en el diagrama que figura en la imagen siguiente. El modo de proceder es similar al seguido en el apartado previo, pues las rutas que se sitúan por debajo necesariamente han de comenzar por el punto $(1,0)$; pero con una salvedad: han de llegar al punto $P(n,n)$ a través del punto $(n,n-1)$, para así efectivamente situarse por debajo de la recta diagonal $y=x$. En el apartado anterior, como $m>n$, no era necesario exigir esta última condición, puesto que el punto $P(m,n)$ se situaba ‘’lejos’’ de la condición que impone la diagonal $y=x$. Así pues, hallaremos el total de rutas comprendidas entre los puntos $(1,0)$ y $(n,n-1)$, para luego sustraer aquellas que intersecan la diagonal $y=x$, utilizando el Principio de reflexión de André.

El número de rutas existente entre los puntos $(1,0)$ y $(n,n-1)$ equivale, por traslación, al total de rutas entre el origen de coordenadas y el punto $(n,n-1) - (1,0) = (n-1,n-1)$, esto es,

$$ C_{2n-2, n-1} = \dbinom{2n-2}{n-1}. $$

Ahora, por el Principio de reflexión de André, el número de trayectorias que van desde el punto $(1,0)$ hasta el punto $(n,n-1)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,1)$ (simétrico de $(1,0)$ respecto de la recta $y=x$) hasta el punto $(n,n-1)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(n,n-1) - (0,1) = (n,n-2)$, esto es,

$$ C_{2n-2,n} = \dbinom{2n-2}{n}. $$

Por tanto, el número de trayectorias desde el origen de coordenadas hasta el punto $P(n,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son

$$ \dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}. $$

Por simetría, el argumento se desarrolla de forma análoga para las trayectorias que se sitúan por encima de la recta diagonal $y=x$, por lo que únicamente hemos de duplicar el anterior resultado alcanzado

$$ 2\left(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\right) $$

para hallar el total de rutas existentes entre el origen de coordenadas y el punto $P(n,n)$ que se sitúan por encima o por debajo de la recta diagonal $y=x$, tocándola únicamente en $O$ y $P(n,n)$.

Finalmente, en el apartado (e), aplicaremos la Regla de Laplace por tratarse de sucesos equiprobables y calcularemos tanto el número de casos favorables, como la cantidad de casos totales, utilizando trayectorias. Para empezar, la cifra de casos totales equivale al número de trayectorias entre el origen de coordenadas y el punto $P(n,n)$, esto es,

$$ C_{2n,n} = \dbinom{2n}{n}. $$

En cuanto al número de casos favorables, precisamente, es el resultado que obtuvimos en el apartado previo. Así,

$$ P = \dfrac{2(C_{2n-2,n-1} - C_{2n-2,n})}{C_{2n,n}} = \dfrac{2\left(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\right)}{\dbinom{2n}{n}} $$

es la probabilidad de obtener $n$ caras y $n$ cruces si la igualdad entre estas no se alcanza antes del último lanzamiento.

Problema 23

Dos candidatos $A$ y $B$ se presentan a una elección. Si $A$ recibe $a$ votos y $B$ recibe $b$ votos, con $a>b$, ¿cuál es la probabilidad de que, en todo momento del escrutinio, $A$ vaya por delante de $B$?

Solución: el presente ejercicio es ciertamente similar a uno de los apartados del anterior problema, por lo que seguiremos el procedimiento allí esbozado. Para empezar, como no tenemos mayores indicaciones sobre cómo transcurre el escrutinio, asumiremos que todos los sucesos posibles de este experimento aleatorio son equiprobables, hecho que nos permitirá calcular probabilidades haciendo uso de la Regla de Laplace.

Por lo que respecta al total de casos posibles, este asciende al número de trayectorias que parten desde el origen de coordenadas y arriban hasta el punto $(a,b)$, que sabemos es

$$ C_{a+b,a} = \dbinom{a+b}{a}. $$

A continuación, de cara a obtener el cardinal del conjunto de casos favorables, sabemos que, a la postre, $a>b$. Por otro lado, la condición de que, durante el escrutinio, el candidato $A$ se mantenga siempre por delante del $B$, se traduce en que las trayectorias que partan del origen de coordenadas y lleguen hasta el punto $(a,b)$, se mantengan siempre por debajo de la diagonal $y=x$, sin intersecarla en momento alguno.

Para ello, las rutas favorables a la situación comentada han de comenzar, necesariamente, desde el punto $(1,0)$. Así pues, hallemos el total de trayectorias existentes entre el punto $(1,0)$ y el punto $(a,b)$ que, por traslación, sabemos es equivalente a la cantidad de rutas entre el origen de coordenadas y el punto $(a,b) - (1,0) = (a-1,b)$ y esta última cifra asciende a

$$ C_{a+b-1,b} = \dbinom{a+b-1}{b}. $$

No obstante, entre ellas habrá algunas que se caractericen por intersecar la recta diagonal $y=x$, que procederemos a sustraer utilizando el Principio de reflexión de André. Aplicado a este caso particular, dicho principio afirma que el número de trayectorias que van desde el punto $(1,0)$ hasta el punto $(a,b)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,1)$ (simétrico de $(1,0)$ respecto de la recta $y=x$) hasta el punto $(a,b)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(a,b) - (0,1) = (a,b-1)$, esto es,

$$ C_{a+b-1,a} = \dbinom{a+b-1}{a}. $$

Por consiguiente, el número de trayectorias desde el origen de coordenadas hasta el punto $(a,b)$, que se sitúan por debajo de la recta diagonal $y=x$, son

$$ \dbinom{a+b-1}{b} - \dbinom{a+b-1}{a}. $$

Finalmente,

$$ P = \dfrac{C_{a+b-1,b} - C_{a+b-1,a}}{C_{a+b,a}} = \dfrac{\dbinom{a+b-1}{b} - \dbinom{a+b-1}{a}}{\dbinom{a+b}{a}} $$

es la probabilidad de que, en todo momento del escrutinio, $A$ vaya por delante de $B$. A modo anecdótico, podemos facilitar una expresión más compacta para $P$. Desarrollando,

$$ \begin{aligned} P &= \dfrac{\dfrac{(a+b-1)!}{b!(a-1)!} - \dfrac{(a+b-1)!}{a!(b-1)!}}{\dfrac{(a+b)!}{a!b!}}\\ &= \dfrac{\dfrac{a(a+b-1)!}{a!b!} - \dfrac{b(a+b-1)!}{a!b!}}{\dfrac{(a+b)!}{a!b!}}\\ &= \dfrac{(a-b)(a+b-1)!}{(a+b)(a+b-1)!} = \dfrac{a-b}{a+b}, \end{aligned} $$

llegamos a una sencilla expresión para rápidamente calcular la probabilidad de interés.

Problemas propuestos

Problema 24:

• (a) ¿Cuántas formas hay de seleccionar $5$ cartas de una baraja de $48$ cartas con reemplazamiento? ¿Y sin reemplazamiento?
• (b) Dadas las letras $a$, $b$, $c$, $d$, $e$, $f$ y $g$, ¿cuántas palabras de cinco letras se pueden formar repitiendo las letras? ¿Y sin repetir?
• (c) Un test consta de $20$ cuestiones con $4$ respuestas cada una, ¿cuántos resultados posibles hay?

Problema 25: seis ladrones tienen a su disposición cuatro calles por las que escapar de la policía, ¿de cuántas maneras pueden hacerlo?

Problema 26: ¿cuántas quinielas de fútbol distintas se pueden hacer?

Problema 27: una mano de bridge consta de $13$ cartas de $52$ de una baraja francesa.

• (a) ¿Cuántas manos de bridge son posibles?
• (b) ¿De cuántas formas se le pueden dar a una persona $6$ picas y $5$ corazones?

Problema 28: $8$ componentes de un equipo se alojan en un hotel. Disponen de una habitación triple, dos dobles y una individual. ¿De cuántas formas pueden repartirse?

Problema 29:

• (a) ¿Cuántos números de $3$ cifras hay? ¿Cuántos son pares?
• (b) ¿Cuántos números capicúas de $5$ cifras hay? ¿Cuántos son pares? ¿Cuántos números capicúas de $6$ cifras existen?

Problema 30:

• (a) Un número telefónico tiene siete cifras enteras. Supongamos que la primera debe ser un número entre $2$ y $9$, ambos inclusive. La segunda y la tercera deben ser números entre $1$ y $9$, ambos inclusive. Cada una de las restantes cifras es un número entre $0$ y $9$, ambos inclusive. ¿Cuántos números de teléfono distintos pueden formarse con estas condiciones?
• (b) Una empresa produce cerraduras de combinación. Cada combinación consta de $3$ números del $0$ al $99$, ambos inclusive. Por el proceso de construcción de las cerraduras, cada número no puede aparecer más de una sola vez en la combinación de la cerradura. ¿Cuántas cerraduras diferentes pueden construirse?

Problema 31:

• (a) ¿Cuántas tiras de longitud $n$, formadas por ceros y unos, contienen exactamente $k$ ceros?
• (b) ¿Cuántas secuencias de $n$ dígitos decimales hay tales que dos dígitos consecutivos sean diferentes?

Problema 32: ¿de cuántas formas se pueden sentar $8$ personas alrededor de una mesa?

Problema 33: en una clase hay $32$ chicos. Cada chico conoce a $5$ chicas de la clase y cada chica conoce a $8$ chicos. ¿Cuántas chicas hay?

Problema 34: ¿de cuántas maneras pueden hacer cola siete ilicitanos y cinco santapoleros si dos santapoleros no pueden estar juntos?

Problema 35: tenemos $5$ libros de geografía, $7$ libros de lengua y $8$ libros de inglés.

• (a) ¿De cuántas maneras se pueden colocar en una estantería?
• (b) ¿De cuántas formas se pueden colocar si deben estar juntos los de la misma asignatura?
• (c) ¿De cuántas maneras se pueden poner si todos los libros de inglés deben estar juntos?

Problema 36: cada usuario de un ordenador tiene una contraseña con una longitud de entre seis y ocho caracteres, cada uno de los cuales es bien un dígito o bien una letra mayúscula. Cada contraseña debe contener al menos un dígito. ¿Cuántas contraseñas distintas admite el sistema?

Problema 37: ¿cuántos números de seis cifras decimales efectivas (sin ceros a la izquierda) pueden formarse de manera que contengan dos o más doses?

Problema 38: encuentra la suma de todos los números capicúas de $5$ cifras.

Problema 39: dados los códigos ordenados de cinco letras entre las ocho: $A$, $B$, $C$, $D$, $E$, $F$, $G$ y $H$ (repetidas o no), se pide

• (a) Número total de códigos.
• (b) Número de ellos con una sola letra repetida dos veces (ejemplo: $ABACH$).
• (c) Número de ellos con dos letras repetidas dos veces cada una (ejemplo: $ABBCA$).
• (d) Número de ellos con una letra repetida tres veces (ejemplo: $AABAE$).
• (e) Número de ellos con una letra repetida tres veces y otra dos (ejemplo: $AABAB$).
• (f) Número de ellos con una letra repetida cuatro veces.
• (g) Número de ellos con una letra repetida cinco veces.
• (h) Número de los que no estén comprendidos entre los apartados (b) a (g).

Problema 40:

• (a) Demuestra que, dadas $367$ personas, al menos dos de ellas cumplen años el mismo día.
• (b) Dados veinte números naturales cualquiera, demuestra que hay al menos dos números cuya diferencia es un múltiplo de $19$.

Problema 41: demuestra que todo número entero $n$ tiene un múltiplo cuya expresión decimal está compuesta de ceros y unos.

Problema 42: en clase, Ana ha dicho $600000$ palabras que tiene entre una y cuatro letras. Dado que el abecedario con el que se expresa posee $27$ letras, ¿ha repetido alguna palabra en su discurso?

Problema 43: demuestra que si repartimos $100$ naranjas en $14$ montones, necesariamente tiene que haber al menos dos montones con el mismo número de naranjas.

Problema 44: para escribir un libro hemos usado $1890$ cifras para numerar las páginas. ¿Cuántas páginas tiene el libro?

Problema 45: ¿es posible disponer sobre una circunferencia los números $0,1,\ldots,9$ de tal manera que la suma de tres números sucesivos cualesquiera sea, como mucho,

• (a) $13$?
• (b) $14$?
• (c) $15$?

Problema 46:

• (a) ¿Cuántos enteros entre $1$ y $1000$, ambos inclusive, son múltiplos de $2$ o de $5$?
• (b) ¿Cuántos enteros entre $1$ y $1000$, ambos inclusive, son primos con $1000$?
• (c) ¿Cuántos enteros entre $1$ y $600$, ambos inclusive, no son divisibles por $3$ ni por $5$ ni por $7$?

Problema 47: entre los números del $1$ al $2000$, halla los que son divisibles por $9$, $11$, $13$ o $15$.

Problema 48: se venden $4$ tipos diferentes de galletas en una tienda. Asumiendo que solo se tiene en cuenta el tipo de galleta y que el orden en que se seleccionan no importa, ¿de cuántas formas se pueden seleccionar $6$ galletas?

Problema 49: ¿de cuántas maneras se pueden poner $9$ como suma de $3$ sumandos enteros positivos?

Problema 50: ¿De cuántas maneras se puede escribir $100$ como suma de $4$ sumandos positivos?

Problema 51: halla el número de soluciones enteras de

• (a) $x_1+x_2+\cdots+x_8=24$, con $x_i\geq 0$, para $i\in{1,2,\ldots,8}$.
• (b) $x_1+x_2+\cdots+x_8=24$, con $x_i\geq 2$, para $i\in{1,2,\ldots,8}$.
• (c) $x+y+z+t = 100$, con $x\geq 30$, $y>21$, $z\geq 1$ y $t\geq 1$.
• (d) $x+y+z+t\leq 2001$, con $x\geq0$, $y\geq 0$, $z\geq 0$ y $t\geq 0$.

Problema 52: en una heladería se sirven $7$ tipos de helados.

• (a) ¿De cuántas formas distintas se pueden elegir $12$ helados?
• (b) ¿De cuántas maneras se pueden elegir $12$ helados si tiene que haber al menos uno de cada tipo?

Problema 53:

• (a) En una tienda de material informático tienen monitores de $4$ marcas diferentes. ¿De cuántas maneras podemos escoger $6$ monitores?
• (b) Queremos repartir $k$ objetos iguales entre los $n$ alumnos que aparecen en una lista. ¿De cuántas maneras podemos hacerlo si queremos que el primer alumno de la lista reciba, como mínimo, $4$ objetos? ¿Y si debe recibir exactamente $4$ objetos?

Problema 54: obtén el número de diagonales que se pueden trazar en un cuadrado, en un hexágono y en un polígono de $n$ lados. ¿Existe algún polígono tal que el número de lado coincida con el número de diagonales?

Problema 55: ¿de cuántas formas pueden distribuirse $12$ libros de idénticos de matemáticas discretas entre cuatro estudiantes?

Problema 56: encuentra la suma de los dígitos de los números del $1$ hasta el $1000$.

Problema 57:

• (a) Encuentra la suma de todos los números capicúas impares de $3$ cifras.
• (b) Encuentra la suma de todos los números capicúas impares de $5$ cifras.

Problema 58: una clase está compuesta por $7$ chicas y $9$ chicos. ¿De cuánta maneras pueden hacer un comité de $5$ personas de forma que

• (a) haya al menos una chica?
• (b) haya como mínimo una chica y un chico?

Problema 59: una mano de bridge consta de $13$ cartas de $52$ de una baraja francesa. ¿De cuántas formas repartiremos el juego entre cuatro personas?

Problema 60: dada una baraja española de $40$ cartas, halla el número de maneras de conseguir las manos especiales del póker.

Problema 61: en un puesto de mando, para transmitir señales, hay en línea recta cuatro astas. En cada asta solamente se puede colocar una bandera. Las señales consisten en colocar banderas de distintos colores en dichas astas. Según el número de banderas colocadas, colores de las mismas y lugar que ocupen, la señal será distinta. Halla el número de señales que se pueden transmitir si se posee un juego de siete banderas con los colores del arco iris.

Problema 62: la lotería primitiva consta de $49$ números. El día del sorteo se eligen $7$ distintos: los $6$ que forman la combinación ganadora y el complementario. En un boleto se pueden marcar $r$ de los $49$ números.

• (a) Marcando $6$ números, ¿cuál es la probabilidad de acertar la combinación ganadora?
• (b) Marcando $6$ números, ¿cuál es la probabilidad de acertar $5$? Realiza la discusión en función del complementario.
• (c) Halla la probabilidad de acertar $5$ números de la combinación ganadora en el caso que haya marcado $10$ de los $49$ posibles.

Problema 63: un desarreglo es una permutación de objetos en la que ningún objeto está en su posición original. Por ejemplo, $234561$ es una permutación de $123456$, pero $213645$ no, ya que $3$ está en su posición original.

• (a) Escribe los desarreglos de $123$.
• (b) Demuestra que, dados $n$ objetos, el total de desarreglos asciende a

$$ D_n = n!\left(1 - \frac{1}{1!} + \frac{1}{2!} - \frac{1}{3!} + \cdots + (-1)^n\cdot\frac{1}{n!}\right). $$

Problema 64: en una fiesta, a la que acuden seis chicos y seis chicas, comienza a sonar la primera canción.

• (a) ¿De cuántas formas pueden organizarse para bailar todos ellos por parejas? Asume que cada pareja está formada por un chico y una chica.
• (b) Como ninguna de las chicas ha quedado contenta con el desempeño en el baile de su pareja, de cara a la segunda canción, ¿de cuántas maneras pueden organizarse para bailar por parejas de forma que no repitan con la anterior?

Problema 65: halla el número de soluciones enteras de la ecuación $x+y+z+t=100$, con $1\leq x\leq 10$, $y\geq 0$, $z\geq 2$ y $20\leq t\leq 30$.

Problema 66: ¿de cuántas maneras podemos sumar $13$ al lanzar $3$ dados?

Problema 67: halla cuántos números de cuatro cifras existen cuya suma de sus cifras ascienda a $27$.

Problema 68: suben dos mujeres y tres hombres a un ascensor en la planta baja de un edificio de seis pisos. Averigua de cuántas maneras se pueden bajar del ascensor, sabiendo que, en un mismo piso, no pueden bajar personas de distinto sexo.

Problema 69: ¿cuántos términos tiene la expansión de $(x_1+x_2+\cdots+x_s)^n$?

Problema 70: calcula

$$ \binom{-2}{3}. $$

Problema 71:

• (a) Calcula, para cada número natural $k$,

$$ \binom{-1}{k}. $$

• (b) Demuestra que, para cada número natural $n$,

$$ \binom{-\frac{1}{2}}{n} = \binom{2n}{n}\cdot\left(-\frac{1}{4}\right)^n. $$

Problema 72: ¿cuántas rutas existen, desde la esquina inferior izquierda de una cuadrícula $n\times n$ a la esquina superior derecha, si los viajes se restringen solo a pasos de longitud unitaria a la derecha o hacia arriba?

Problema 73: dada una cuadrícula $n\times n$, sobre la que nos podemos desplazar con pasos unitarios hacia la derecha o hacia arriba, se dice que una ruta es ‘‘buena’’ si va por debajo de la diagonal y la toca.

• (a) ¿Cuántas rutas ‘‘buenas’’ hay?
• (b) Escogida una ruta al azar de la cuadrícula, ¿cuál es la probabilidad de que sea ‘‘buena’’?

Problema 74: sea el plano $E$ cuadriculado por las rectas $x=m$ e $y=n$, con $m$ y $n$ números enteros. El punto $P(m,n)$ es un nudo de la cuadrícula. Una sucesión de nudos se llama trayectoria. Se consideran las trayectorias ascendentes $T_a$ en las que se pasa de un nudo al siguiente por la traslación $u$ o por la traslación $v$, donde $(O,u,v)$ es un sistema ortogonal. La longitud de una trayectoria es el número de traslaciones $u$ o $v$ que tiene.

• (a) Determina el número $T_a(O,P)$ que van del origen $O$ al punto $P(m,n)$ ($m\geq0, n\geq0$) y el número de trayectorias $T’_a(P’,P)$ que van del punto $P’(m’,n’)$ al punto $P(m,n)$ con $m’\leq m$ y $n’\leq n$.
• (b) Calcula el número de trayectorias de longitud $h$, $T_a$, que parten del origen.
• (c) Sea $P(m,n)$, con $m>n$. Calcula el número $T_{a_1}(O,P)$ de trayectorias que van de $O$ a $P$ por debajo de la diagonal $y=x$.
• (d) Sea $P(n,n)$. Halla el número de trayectorias $T_{a_2}(O,P)$ que van de $O$ a $P$ por encima o por debajo de la diagonal principal sin tocarla más que en los puntos $O$ y $P$.
• (e) Se lanza una moneda $2n$ veces, ¿cuál es la probabilidad de obtener $n$ caras y $n$ cruces? Se supone que la igualdad no se alcanza antes del último lanzamiento.

Problema 75: en la cola del cine hay $2n$ personas que deben comprar una entrada de $5$ euros. Hay $n$ personas que tienen un billete de $5$ euros y hay $n$ personas que tienen un billete de $10$ euros. Si la persona que está en caja no dispone de cambio al principio, determina la probabilidad de que ningún cliente tenga que esperar para recibir la vuelta.

Problema 76: un grupo de $n+m$ personas se alinean frente a las taquillas de un teatro para comprar una entrada cuyo precio es de $50$ euros. De entre ellas, $m$ poseen un billete de $50$ euros, mientras que $n$ poseen un billete de $100$ euros ($m\geq n$). Al abrir la taquilla, el cajero no tiene cambio. ¿Cuál es la probabilidad de que estas personas se alineen de manera que el cajero siempre tenga cambio?

Problema 77: dos candidatos $A$ y $B$ se presentan a una elección. Si $A$ recibe $a$ votos y $B$ recibe $b$ votos, con $a>b$,

• (a) ¿cuál es la probabilidad de que, en todo momento del escrutinio, $A$ vaya por delante de $B$?
• (b) ¿Cuál es la probabilidad de que, a lo largo del escrutinio, la diferencia de votos a favor de $A$ no haya sido mayor que $a-b$?

Problema 78: se sabe que una elección, para la cual hay dos candidatos $A$ y $B$, ha terminado con el resultado de $9$ votos a favor de $A$ y $6$ a favor de $B$. Calcula:

• (a) la probabilidad de que, durante el escrutinio de los votos, siempre haya ido por delante el candidato $A$.
• (b) la probabilidad de que, a lo largo del escrutinio, la diferencia entre los dos candidatos no haya sido superior a $3$.

Problema 79: en una cuadrícula de tamaño $8\times 8$ hay dos hormigas, $A$ y $B$, ubicadas en las esquinas opuestas. La hormiga $A$ (situada en la esquina inferior izquierda) se mueve en pasos de longitud unitaria hacia la derecha o hacia arriba, mientras que la hormiga $B$ hace lo propio hacia la izquierda o hacia abajo. ¿Cuál es la probabilidad de que se encuentren? Asume que ambas caminan a la misma velocidad y empiezan a hacerlo simultáneamente.

Problema 80: un avión, de una determinada compañía, debe realizar un viaje entre dos ciudades, con un total de $m+n$ escalas, donde $m$ y $n$ son números naturales. En cada escala el avión ha de cargar o descargar una tonelada de cierta mercancía, realizando cargas en $m$ de las escalas y descargas en las $n$ restantes.

No obstante, en la compañía nadie ha reparado en que el avión no soporta una carga mayor de $k$ toneladas, con $k$ número natural entre $n$ y $m+n$, y las escalas de carga y descarga se reparten al azar.

Si el avión sale con $n$ toneladas de mercancía, calcula la probabilidad de que llegue a su destino.

Problema 81: la Rana Gustavo, ‘’el reportero más dicharachero’’, se encuentra en su hogar (muy coqueto este y ubicado, por cierto, en el origen de coordenadas, $(0,0)$, de una cuadrícula plana) disfrutando de su serie favorita. De repente, recibe una notificación en su móvil: ha de acudir, ipso facto, a cubrir una importante noticia que ha tenido lugar en la panadería de Barrio Sésamo, que se halla, según el GPS, en el punto de la cuadrícula de coordenadas $(5,5)$.

Por ciertos problemas acotencidos durante la última retransmisión, la Rana Gustavo únicamente puede desplazarse mediante saltos de longitud unitaria bien hacia la derecha, bien hacia arriba.

• (a) Calcula el número total de rutas existentes entre su casa y la panadería de Barrio Sésamo.
• (b) En el punto de la cuadrícula de coordenadas $(2,2)$, está plácidamente Espinete tomando el sol. La Rana Gustavo no quiere entretenerse hablando con él, pues tiene mucha prisa por cubrir la noticia, ¿de cuántas maneras puede llegar a la panadería sin pasar por donde está Espinete?
• (c) Resulta, además, que Coco está esperando, en el punto de la cuadrícula de coordenadas $(3,3)$, a la primera persona que pase por allí para jugar una partida de ajedrez. Como la Rana Gustavo no está por la labor de tales entretenimientos, ¿de cuántas formas puede llegar a la panadería sin pasar por donde está Espinete ni por donde está Coco?

Problema 82: un jugador lanza una moneda. Si sale cara obtiene un punto positivo y si saca cruz un punto negativo. Supuesto que de entrada se le da un punto positivo y perderá cuando alcance una puntuación nula, calcula la probabilidad de perder:

• (a) antes del lanzamiento $12$.
• (b) en el lanzamiento $17$.