 Fotografía de Piermanuele Sberni, disponible en Unsplash.
Fotografía de Piermanuele Sberni, disponible en Unsplash.
Problema 79: ¿Cuántas rutas existen, desde la esquina inferior izquierda de una cuadrícula $n\times n$ a la esquina superior derecha, si los viajes se restringen solo a pasos de longitud unitaria a la derecha o hacia arriba?
Antes de abordar el problema en su versión general, tal y como reza el enunciado, estudiemos un caso concreto, como el que se muestra en la siguiente figura. En ella, hemos tomado $n=5$ y sobre la cuadrícula aparecen delineadas dos de las posibles rutas (una en verde y otra en rojo) que parten del origen de coordenadas $(0,0)$ y llegan hasta el punto $(5,5)$. Esto es, ambas parten desde la esquina inferior izquierda de la mencionada cuadrícula y arriban a su esquina superior derecha.
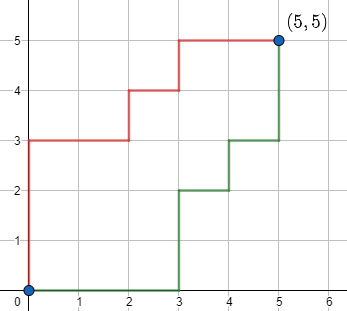
Si denotamos por $D$ a los pasos de longitud unitaria que se recorren hacia la derecha y por $A$ a los correspondientes que se efectúan hacia arriba, rápidamente apreciamos que, en cada una de las rutas que podamos imaginar, habrá cinco $D$ y otras cinco $A$. Es decir, toda ruta es una reordenación de la cadena $DDDDDAAAAA$. El número de tales cadenas que podemos escribir asciende al total de permutaciones con repetición de diez elementos, donde uno de ellos se repite cinco veces, mientras que el otro lo hace en el mismo número de ocasiones. Así, hay
$$ PR_{10}^{5,5} = \dfrac{10!}{5!5!} = \dfrac{10\cdot9\cdot8\cdot7\cdot6}{5!} = 252 $$
rutas posibles cuando $n=5$.
Alternativamente, podemos enfocar el problema como sigue: para llegar desde una esquina a la otra es necesario que efectuemos un total de diez de pasos, de los cuales cinco habrán de ser hacia la derecha (el mismo razonamiento es válido si consideramos dar los pasos hacia arriba). Como el orden en el que los demos no es importante, el número de maneras de dar cinco pasos a la derecha de un total de diez pasos equivale al total de combinaciones de diez elementos tomados de cinco es cinco, es decir,
$$ C_{10,5} = \dbinom{10}{5} = \dfrac{10\cdot9\cdot8\cdot7\cdot6}{5!} = 252. $$
Si ahora consideramos una cuadrícula rectangular, de manera que la esquina superior derecha de la misma la situamos en el punto $(5,7)$, razonaríamos de manera análoga a como hicimos en el párrafo anterior. ¿Cuántos pasos hemos de efectuar para llegar desde el origen de coordenadas hasta el punto $(5,7)$? En las condiciones que impone el enunciado del ejercicio, serían $5+7=12$ los pasos requeridos. El número de rutas, entonces, ascendería al total de combinaciones de doce elementos tomados de cinco en cinco, $C_{12,5}$ (o bien $C_{12,7}$ si hacemos el razonamiento fijándonos en los pasos que deben darse hacia arriba), esto es,
$$ C_{12,5} = C_{12,7} = \dbinom{12}{5} = \dfrac{12\cdot11\cdot10\cdot9\cdot8}{5!} = 792 $$
son las rutas posibles en este caso.
En general, dada una cuadrícula $m\times n$ el número de rutas que existen, desde su esquina inferior izquierda hasta su esquina superior derecha, si los viajes se restringen a pasos de longitud unitaria a la derecha o hacia arriba asciende a
$$ C_{m+n,n} = \dbinom{m+n}{n}\qquad\text{o}\qquad C_{m+n,m}=\dbinom{m+n}{m}. $$
En nuestro caso concreto, como $m=n$, dicha cifra será
$$ C_{2n,n} = \dbinom{2n}{n}. $$
Imaginemos, a continuación, que nos indican que estamos situados en el punto $(1,2)$. ¿Cuántas rutas distintas existen desde dicho punto a la esquina superior derecha de la cuadrícula, $(n,n)$? Esta cuestión la resolveríamos aplicando una traslación, puesto que el número de rutas entre los puntos $(1,2)$ y $(n,n)$ equivale al total de rutas entre $(0,0)$ y $(n-1,n-2)$ (simplemente hemos efectuado una traslación de vector $(1,2)$, es decir, sustraemos el mencionado vector a ambos puntos para obtener los finalmente mostrados). Dicha cifra, aplicando lo visto en párrafos anteriores, será
$$ \dbinom{n-1+n-2}{n-1} = \dbinom{2n-3}{n-1} = C_{2n-3,n-1} $$
o bien $C_{2n-3,n-2}$.
Consideremos ahora que la longitud de una ruta equivale al número de pasos realizados. Así, podríamos preguntamos, ¿cuántas rutas de longitud seis existen? Una ruta de longitud seis, en las condiciones que impone en el enunciado de este ejercicio, puede llevarnos a cualquiera de los puntos que se indican en la siguiente figura, por lo que la tarea se reduce entonces a contar el número de rutas existente desde el origen de coordenadas a cada uno de ellos.
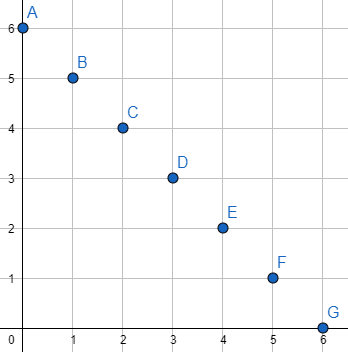
Así, de $(0,0)$ a $(0,6)$ hay un total de $C_{6,0}$ rutas; de $(0,0)$ a $(1,5)$ encontramos $C_{6,1}$ rutas; de $(0,0)$ a $(2,4)$ hallamos $C_{6,2}$ rutas; y así sucesivamente. En total son
$$ \dbinom{6}{0} + \dbinom{6}{1} + \dbinom{6}{2} + \dbinom{6}{3} + \dbinom{6}{4} + \dbinom{6}{5} + \dbinom{6}{6} = 2^6 = 64, $$
ya que,
$$ \dbinom{n}{0} + \dbinom{n}{1} + \dbinom{n}{2} + \cdots + \dbinom{n}{n} = \sum_{k=0}^{n}{\dbinom{n}{k}} = (1+1)^n = 2^n. $$
Por tanto, si ahora nos preguntasen por el total de rutas de longitud diez, directamente podríamos decir que son $2^{10} = 1024$.
Este clásico problema, conocido como el de las rutas equiprobables, nos permite dar respuesta a preguntas como: ¿de cuántas maneras podemos obtener cinco caras y cinco cruces al lanzar una moneda diez veces? En ejercicios anteriores, utilizando técnicas de combinatoria, hallamos que dicha cantidad equivalía a $PR_{10}^{5,5}$ o bien $C_{10,5}$. Un enfoque alternativo sería por conteo de rutas desde el origen de coordenadas hasta el punto de interés, $(5,5)$ en esta ocasión. Por otro lado, el total de rutas de longitud seis es, en otros términos, la cantidad de secuencias que podemos obtener al lanzar una moneda seis veces, que, por combinatoria, sabemos asciende a $VR_{2,6} = 2^6 = 64$. Así, los ejercicios de rutas fácilmente se extrapolan a otros contextos (sobre todo de monedas) y podemos resolver con ellas interrogantes del estilo: dado que he obtenido una cada y dos cruces, ¿de cuántas formas posibles puedo llegar a conseguir diez caras y diez cruces? La respuesta, como vimos en párrafos anteriores, la encontraríamos rápidamente tras aplicar una traslación de vector $(1,2)$ y contar después del número de rutas entre el origen de coordenadas y el punto $(9,8)$.