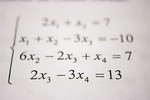Problemas (Oposición)
Fotografía de Antoine Dautry, disponible en Unsplash.
A nivel personal, de las cuatro partes en que se divide el procedimiento de selección de oposiciones, la asociada al supuesto práctico es aquella que encuentro más interesante. Cierto es que con un temario tan extenso como variado, esta parte precisa una buena dedicación de tiempo para preparala con garantías.
En este proyecto, por tanto, recogeré diversos problemas matemáticos enfocados a la preparación de oposiciones. Por comodidad, los agruparé por temática en la siguiente tabla:
| Temática | Problema |
|---|---|
| Combinatoria | 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81 |
| Complejos | 4 |
| Determinantes | 2 |
| Ecuaciones | 57 |
| Ecuaciones diofánticas | 11, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 58 |
| Ecuaciones en diferencias | 12, 13, 14, 15, 16 |
| Inducción | 1, 5, 6, 7, 8, 9 |
| Teoría de números | 3, 10, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44 |
