 Fotografía de Carlos ‘Grury’ Santos, disponible en Unsplash.
Fotografía de Carlos ‘Grury’ Santos, disponible en Unsplash.
Problema 80: Sea el plano $E$ cuadriculado por las rectas $x=m$ e $y=n$, con $m$ y $n$ números enteros. El punto $P(m,n)$ es un nudo de la cuadrícula. Una sucesión de nudos se llama trayectoria. Se consideran las trayectorias ascendentes $T_a$ en las que se pasa de un nudo al siguiente por la traslación $u$ o por la traslación $v$, donde $(O,u,v)$ es un sistema ortogonal. La longitud de una trayectoria es el número de traslaciones $u$ o $v$ que tiene.
- (a) Determina el número $T_{a}(O,P)$ que va desde el origen $O$ hasta el punto $P(m,n)$ ($m\geq0$, $n\geq0$) y el número de trayectorias $T^{\prime}_{a}( P^{\prime}, P )$ que van del punto $P^{\prime} ( m^{\prime}, n^{\prime} )$ al punto $P(m,n)$ con $m^{\prime}\leq m$ y $n^{\prime}\leq n$.
- (b) Calcula el número de trayectorias de longitud $h$, $T_a$, que parten del origen.
- (c) Sea $P(m,n)$, con $m>n$. Calcula el número $T_{a_1}(O,P)$ de trayectorias que van de $O$ a $P$ por debajo de la diagonal $y=x$.
- (d) Sea $P(n,n)$. Halla el número de trayectorias $T_{a_2}(O,P)$ que van de $O$ a $P$ por encima o por debajo de la diagonal principal sin tocarla nada más que en los puntos $O$ y $P$.
- (e) Se lanza una moneda $2n$ veces, ¿cuál es la probabilidad de obtener $n$ caras y $n$ cruces? Se supone que la igualdad no se alcanza antes del último lanzamiento.
El presente problema, en planteamiento, es similar (en parte) al que figura en el problema anterior, de manera que haremos uso aquí de algunos de los resultados alcanzados allí. Así, la situación que se plantea queda ilustrada en el siguiente diagrama.
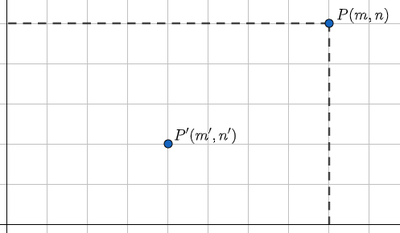
En el apartado (a) nos piden obtener el número de trayectorias (que en el ejercicio anterior designábamos por rutas) desde el origen de coordenadas hasta el punto $P(m,n)$. Sabemos que dicha cifra se corresponde con la elección de $m$ posibilidades tomadas de un total de $m+n$, esto es,
$$ C_{m+n,m} = \dbinom{m+n}{m}, $$
cantidad que es equivalente, asimismo, a $C_{m+n,n}$ o a $PR_{m+n}^{m,n}$.
A continuación, para la segunda parte de este apartado, hemos de encontrar el total de rutas existentes entre los puntos $P^{\prime} ( m^{\prime}, n^{\prime} )$ y $P(m,n)$. Dicha cifra es equivalente, por traslación, al número de rutas entre el origen de coordenadas y el punto $(m,n) - ( m^{\prime}, n^{\prime} ) = ( m - m^{\prime}, n - n^{\prime} )$. Por tanto, hay
$$ C_{m+n-m^{\prime}-n^{\prime}, m-m^{\prime}} = \dbinom{m+n-m^{\prime}-n^{\prime}}{m-m^{\prime}} $$
rutas existentes entre los puntos $P^{\prime} ( m^{\prime}, n^{\prime} )$ y $P(m,n)$.
Para el apartado (b), por el razonamiento que se encuentra en el ejercicio citado, concluimos que el número de trayectorias de longitud $h$ es
$$ \dbinom{h}{0} + \dbinom{h}{1} + \dbinom{h}{2} + \cdots + \dbinom{h}{h} = 2^h. $$
Acto seguido, para el apartado (c), nos apoyaremos en el diagrama que aparece en la siguiente figura, donde hemos añadido al anterior la recta diagonal de ecuación $y=x$.
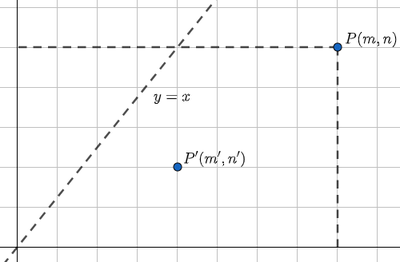
Buscamos todas las rutas existentes entre el origen de coordenadas y el punto $P(m,n)$ que se sitúen por debajo de la mencionada diagonal, esto es, que no posean intersección con ella. Obligatoriamente, todas ellas empezarán desde el punto $(1,0)$, ya que de hacerlo desde $(0,1)$, parte de la ruta se situaría por encima de la diagonal $y=x$.
Así pues, hallemos el total de rutas existentes entre el punto $(1,0)$ y el punto $P(m,n)$ que, por traslación, sabemos es equivalente a la cantidad de rutas entre el origen de coordenadas y el punto $(m,n) - (1,0) = (m-1,n)$ y esta última cifra asciende a
$$ C_{m+n-1,n} = \dbinom{m+n-1}{n}. $$
No obstante, entre ellas habrá algunas que se caractericen por intersecar la diagonal $y=x$, que procedemos a sustraer utilizando el Principio de reflexión de André. Aplicado a este caso particular, dicho principio afirma que el número de trayectorias que van desde el punto $(1,0)$ hasta el punto $P(m,n)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,1)$ (simétrico de $(1,0)$ respecto de la recta $y=x$) hasta el punto $P(m,n)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (0,1) = (m,n-1)$, esto es,
$$ C_{m+n-1,m} = \dbinom{m+n-1}{m}. $$
Por consiguiente, el número de trayectorias desde el origen de coordenadas hasta el punto $P(m,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son
$$ \dbinom{m+n-1}{n} - \dbinom{m+n-1}{m}. $$
Siendo estrictos, en realidad el primer punto de partida es $(2,0)$ y no $(1,0)$, puesto que si de este último efectuamos un ‘‘paso hacia arriba’’ se produciría una intersección con la recta diagonal $y=x$. No obstante, el Principio de reflexión de André nos permite empezar, sin problema alguno, desde $(1,0)$, ya que descontará las rutas que no satisfagan la condición impuesta en el enunciado para este apartado. No obstante, si optamos por empezar desde $(2,0)$, el procedimiento a seguir es análogo al mostrado en párrafos anteriores. El total de rutas de rutas desde el punto $(2,0)$ al punto $P(m,n)$, por traslación, equivale a la cantidad de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (2,0) = (m-2,n)$, esto es,
$$ C_{m+n-2,n} = \dbinom{m+n-2}{n}. $$
Ahora, por el Principio de reflexión de André, el número de trayectorias que van desde el punto $(2,0)$ hasta el punto $P(m,n)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,2)$ (simétrico de $(2,0)$ respecto de la recta $y=x$) hasta el punto $P(m,n)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(m,n) - (0,2) = (m,n-2)$, esto es,
$$ C_{m+n-2,m} = \dbinom{m+n-2}{m}. $$
Por tanto, el número de trayectorias desde el origen de coordenadas hasta el punto $P(m,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son
$$ \dbinom{m+n-2}{n} - \dbinom{m+n-2}{m}, $$
y esta diferencia coincide con la calculada anteriormente.
En el apartado (d), la situación se ilustra en el diagrama que figura en la imagen siguiente. El modo de proceder es similar al seguido en el apartado previo, pues las rutas que se sitúan por debajo necesariamente han de comenzar por el punto $(1,0)$; pero con una salvedad: han de llegar al punto $P(n,n)$ a través del punto $(n,n-1)$, para así efectivamente situarse por debajo de la recta diagonal $y=x$. En el apartado anterior, como $m>n$, no era necesario exigir esta última condición, puesto que el punto $P(m,n)$ se situaba ‘‘lejos’’ de la condición que impone la diagonal $y=x$. Así pues, hallaremos el total de rutas comprendidas entre los puntos $(1,0)$ y $(n,n-1)$, para luego sustraer aquellas que intersecan la diagonal $y=x$, utilizando el Principio de reflexión de André.
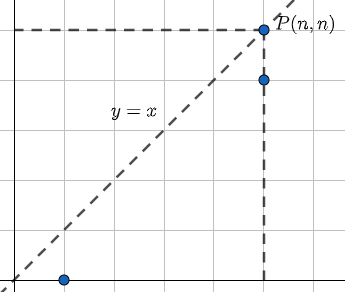
El número de rutas existente entre los puntos $(1,0)$ y $(n,n-1)$ equivale, por traslación, al total de rutas entre el origen de coordenadas y el punto $(n,n-1) - (1,0) = (n-1,n-1)$, esto es,
$$ C_{2n-2, n-1} = \dbinom{2n-2}{n-1}. $$
Ahora, por el Principio de reflexión de André, el número de trayectorias que van desde el punto $(1,0)$ hasta el punto $(n,n-1)$ e intersecan la recta diagonal $y=x$, equivale a la cantidad de trayectorias que van desde el punto $(0,1)$ (simétrico de $(1,0)$ respecto de la recta $y=x$) hasta el punto $(n,n-1)$. Por traslación, estas equivalen al total de trayectorias desde el origen de coordenadas hasta el punto $(n,n-1) - (0,1) = (n,n-2)$, esto es,
$$ C_{2n-2,n} = \dbinom{2n-2}{n}. $$
Por tanto, el número de trayectorias desde el origen de coordenadas hasta el punto $P(n,n)$, que se sitúan por debajo de la recta diagonal $y=x$, son
$$ \dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}. $$
Por simetría, el argumento se desarrolla de forma análoga para las trayectorias que se sitúan por encima de la recta diagonal $y=x$, por lo que únicamente hemos de duplicar el anterior resultado alcanzado
$$ 2\left(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\right) $$
para hallar el total de rutas existentes entre el origen de coordenadas y el punto $P(n,n)$ que se sitúan por encima o por debajo de la recta diagonal $y=x$, tocándola únicamente en $O$ y $P(n,n)$.
Finalmente, en el apartado (e), aplicaremos la Regla de Laplace por tratarse de sucesos equiprobables y calcularemos tanto el número de casos favorables, como la cantidad de casos totales, utilizando trayectorias. Para empezar, la cifra de casos totales equivale al número de trayectorias entre el origen de coordenadas y el punto $P(n,n)$, esto es,
$$ C_{2n,n} = \dbinom{2n}{n}. $$
En cuanto al número de casos favorables, precisamente, es el resultado que obtuvimos en el apartado previo. Así,
$$ P = \dfrac{2(C_{2n-2,n-1} - C_{2n-2,n})}{C_{2n,n}} = \dfrac{2\left(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\right)}{\dbinom{2n}{n}} $$
es la probabilidad de obtener $n$ caras y $n$ cruces si la igualdad entre estas no se alcanza antes del último lanzamiento.