Fotografía de Julian Hochgesang, disponible en Unsplash.
Problema 69: Obtén el número de diagonales que se pueden trazar en un cuadrado, en un hexágono y en un polígono de $n$ lados. ¿Existe algún polígono tal que el número de lados coincide con el número de diagonales?
A la vista de la figura siguiente, por recuento, concluimos que un cuadrado posee dos diagonales, mientras que en un hexágono el número de diagonales asciende a nueve.
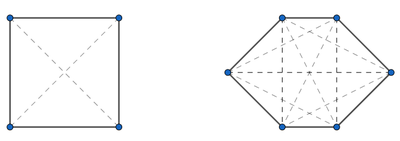
En general, para poder dibujar una diagonal necesitamos unir dos de los vértices del correspondiente polígono, por lo que hemos de ser capaces de averiguar el número de formas en que podemos seleccionar los mencionados dos vértices. Como no importa el orden en el que los escojamos, el total equivale a la cantidad de combinaciones de $n$ elementos tomados de dos en dos, esto es, a $C_{n,2}$. No obstante, hemos de actuar con cautela, puesto que, de la manera indicada, estaríamos considerando como diagonal también la unión de dos vértices contiguos, es decir, cada uno de los lados. Así pues, sustrayendo estos, la cantidad de diagonales de un polígono de $n$ lados asciende a
$$ C_{n,2} - n = \dbinom{n}{2} - n = \dfrac{n(n-1)}{2} - n = \dfrac{n^2-n-2n}{2} = \dfrac{n^2-3n}{2}. $$
Alternativamente, fijado un vértice del polígono de $n$ lados, generamos diagonales si lo unimos con los vértices que no le son contiguos, es decir, con los restantes $n-3$ vértices. Así, cada vértice posee asociadas $n-3$ diagonales. Como contamos con $n$ vértices, aplicando la regla del producto, hablaríamos de un total de $n(n-3)$ diagonales. Sin embargo, procediendo así, debemos pensar que cada diagonal se cuenta en dos ocasiones, de manera que, corrigiendo por dicho factor, el total de diagonales de un polígono de $n$ lados es
$$ \dfrac{n(n-3)}{2} = \dfrac{n^2 -3n}{2} $$
como antes.
Ahora, para dar respuesta a la pregunta planteada en el enunciado del ejercicio, igualando el total de diagonales de un polígono de $n$ lados con su número de lados, tenemos
$$ \dfrac{n^2 -3n}{2} = n. $$
Es decir, se conforma la ecuación $n^2 -3n=2n$ o, equivalentemente, $n^2 -5n=0$. Esta posee dos soluciones, la trivial, $n=0$, que rechazamos por no conformar un polígono propiamente dicho; y $n=5$, esto es, el pentágono es el único polígono cuyo número de lados coincide con su cantidad de diagonales.
