 Fotografía de Ketan Krishnan, disponible en Unsplash.
Fotografía de Ketan Krishnan, disponible en Unsplash.
Problema 75: Trazamos en un plano $n$ rectas secantes dos a dos, pero tres a tres no concurrentes, ¿en cuántas regiones queda dividido el plano?
Claramente observamos, en la siguiente imagen, que dos rectas secantes dividen el plano en cuatro regiones. Al añadir una nueva recta, de manera que las tres no sean concurrentes en un punto, necesariamente aparecerán dos nuevos puntos de intersección con las rectas originales (puesto que la incorporada no puede ser paralela a las existentes, al existir la restricción de que las rectas sean secantes dos a dos), hecho que implica que la recta subdivide en dos tres de las cuatro regiones en las que se encontraba dividido el plano, produciendo entonces en total siete regiones ($4 + 3 = 7$).
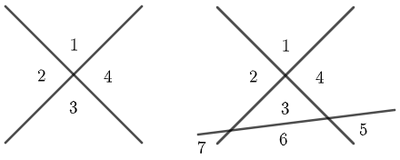
Una cuarta recta, que fuese secante dos a dos con las tres anteriores, daría lugar a tres nuevos puntos de intersección, situación que provocaría que cuatro de las anteriores regiones quedasen, cada una de ellas, subdividas en dos nuevas regiones. En total, contaríamos pues con once regiones ($7 + 4 = 11$).
En general, denotemos por $R_n$ al número de regiones en que el plano queda dividido por $n$ rectas que son secantes dos a dos, pero tres a tres no concurrentes. Al incorporar una nueva recta, que será secante dos a dos con todas las anteriores, esta dará lugar a $n$ nuevos puntos de intersección (ya que no será concurrente tres a tres con ninguno de los pares presentes), hecho que provoca que, de las $R_n$ regiones que se contaban antes de introducir la nueva recta, $n+1$ queden, cada una de ellas, subdividas en dos regiones. Así, es cierto que, para cada número natural $n$,
$$ R_{n+1} = R_n + (n+1), $$
dando lugar a una ecuación en diferencias lineal completa de orden uno. Su ecuación homogénea asociada es $R_{n+1} - R_n = 0$, con ecuación característica correspondiente $\lambda - 1 = 0$, esto es, $\lambda = 1$. Así, la solución para dicha ecuación homogénea es $R_h = c_1$, con $c_1\in\mathbb{R}$.
Ahora, como el término independiente, $n+1$, es un polinomio de grado uno en $n$ y $\lambda = 1$ es una raíz simple de la ecuación característica, proponemos como solución particular $n^1(an+b) = an^2+bn$ y sustituyendo en la ecuación en diferencias inicial, queda
$$ a(n+1)^2 + b(n+1) - an^2 - bn = n+1. $$
Operando, llegamos a que $2an + (a+b) = n+1$ e igualando coeficientes $a = b = 1 / 2$, por lo que la solución particular a la ecuación en diferencias planteada es, para cada número natural $n$, $R_p = (n^2+n) / 2$.
Por consiguiente, la solución general a la ecuación en diferencias propuestas, que es la suma de la solución para la ecuación homogénea y la solución particular, es
$$ R_n = c_1 + \dfrac{n^2+n}{2}, $$
con $c_1\in\mathbb{R}$. Dado que para $n = 2$ hemos establecido, al principio del ejercicio, que $R_2 = 4$, sustituyendo podemos averiguar el valor de $c_1$. Así,
$$ 4 = c_1 + \dfrac{2^2+2}{2}, $$
esto es, $c_1 = 1$ y concluimos que, para cada número natural $n$,
$$ R_n = \dfrac{n^2+n+2}{2} $$
es el número de regiones en que queda dividido un plano cuando trazamos $n$ rectas secantes dos a dos, pero tres a tres no concurrentes.
Alternativamente, por tanteo de unos cuantos casos particulares para los primeros valores de $n$, obtenemos la siguiente tabla
| $n$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
|---|---|---|---|---|---|---|
| $R_n$ | $2$ | $4$ | $7$ | $11$ | $16$ | $22$ |
| $\Delta R_n$ | $2$ | $3$ | $4$ | $5$ | $6$ | $7$ |
| $\Delta^2 R_n$ | $1$ | $1$ | $1$ | $1$ | $1$ | $1$ |
Por consiguiente, la sucesión $(R_n)$ es una progresión aritmética de orden dos, luego, por los resultados teóricos asociados a este tipo de sucesiones,
$$ \begin{aligned} R_n &= \dbinom{n-1}{0}R_1 + \dbinom{n-1}{1}\Delta R_1 + \dbinom{n-1}{2}\Delta^2 R_1\\ &= 1\cdot2 + (n-1)\cdot2 + \dfrac{(n-1)(n-2)}{2}\cdot1\\ &= \dfrac{4 + 4(n-1) + (n-1)(n-2)}{2}\\ &= \dfrac{n^2 +n+2}{2}, \end{aligned} $$
arribando al mismo resultado que antes.