Fotografía de Clark Van Der Beken, disponible en Unsplash.
Nueva entrega de enunciados propuestos de cara a la preparación de oposiciones para la especialidad de matemáticas. La colección completa está disponible aquí.
Ejercicio 1: Para detectar la presencia de cierta enfermedad en un individuo perteneciente a una población determinada, se emplea un análisis tal que la probabilidad de que dé positivo, si el individuo analizado tiene realmente la enfermedad, es $0.96$. Se sabe que el $2\%$ de los individuos de dicha población padecen la enfermedad; por otro lado, se ha llegado a establecer que, realizado el análisis sobre todos los individuos de la población, daría positivo en el $2.5\%$ de los casos.
- (a) Calcula la probabilidad de que un individuo, cuyo análisis ha dado positivo, padezca la enfermedad en cuestión.
- (b) Calcula la probabilidad de que, al realizar el análisis a un individuo determinado, el diagnóstico resulte equivocado.
Ejercicio 2: Calcula el valor de $\sqrt[3]{8 + 3\sqrt{21}} + \sqrt[3]{8 - 3\sqrt{21}}$.
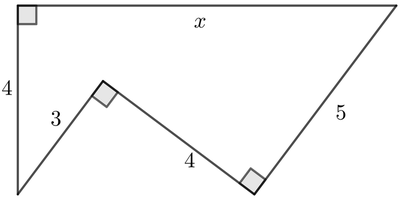
Ejercicio 3: Dada la figura, halla el valor de $x$.
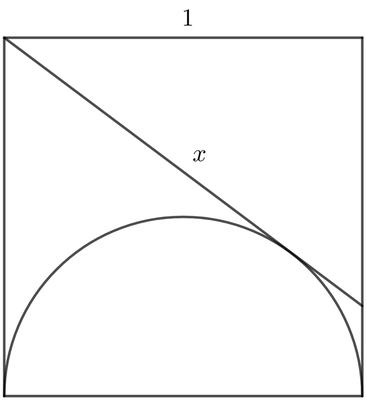
Ejercicio 4: Dado un cuadrado, cuyo lado mide una unidad, halla la longitud del segmento $x$ que aparece en la figura, tangente a la semicircunferencia inscrita.
Ejercicio 5: Resuelve en $\mathbb{Z}$ la ecuación $x^2 + x - 2\equiv 0\pmod{13}$.
Ejercicio 6: Una banda de piratas se apodera de un botín de piezas de oro iguales. Deciden repartírselo a partes iguales y el resto dárselo al cocinero chino, que recibe en este caso $3$ piezas. Los piratas pelean entre sí y mueren seis de ellos, con lo que en el nuevo reparto el cocinero chino se lleva $4$ piezas de oro. De regreso, el barco se hunde y se salvan el botín, seis piratas y el cocinero chino inmortal, con lo que el nuevo reparto le da ahora $5$ piezas al cocinero chino. ¿Cuál es la fortuna esperada por el cocinero chino cuando decide matar al resto de los piratas para quedarse el botín él solo si la banda era de $17$ piratas?
